8. F modeling#
Traction — compression pure elastoplastic behavior that is damaging (GLRC_DM + Von Mises).
In this test, we are interested in elastoplastic behavior. We can insert plastic behavior to the answer of model GLRC_DMvia, a « kit » that makes it possible to put model GLRC_DMavec into series, a classical Von Mises plastic model. This kit consists in imposing the same stress tensor on both models and in combining the two deformation tensors.
8.1. Characteristics of modeling#
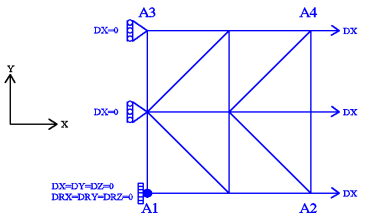
Figure 8.1-a: mesh and boundary conditions
Modeling: DKTG. \(L=1.0m\).
Boundary conditions:
Embedding in \({A}_{1}\);
\(\mathrm{DX}=0.0\) on the \({A}_{1}-{A}_{3}\) edge;
\(\mathrm{DX}={U}_{0}\times f(t)\) on the \({A}_{2}-{A}_{4}\) edge;
where \({U}_{0}=3.0\times {10}^{-3}m\) and \(f(t)\) represent the magnitude of cyclic loading as a function of the (pseudo-time) parameter \(t\) as follows:
Integration increment: \(\mathrm{8,50}\times {10}^{-3}s\).
8.2. Characteristics of the mesh#
Number of knots: 9
Number of stitches: 8 TRIA3; 8 SEG2.
8.3. Tested sizes and results#
Identification |
Reference Type |
Reference Value |
Tolerance |
|
At \(t=\mathrm{0,017}\) traction - elastic phase |
||||
Movement \(\mathrm{DY}\) en \(\mathrm{A4}\) |
|
1.44237 10-2 |
1 10-4 |
|
Membrane effort \({N}_{\mathrm{xx}}\) en \(\mathrm{A4}\) |
|
0 |
5 10-3 |
|
At \(t=\mathrm{0,085}\) traction - damage phase |
||||
Move \(\mathrm{DY}\) en \(\mathrm{A4}\) |
|
-4.84715 10-1 |
1 10-4 |
|
Membrane effort \({N}_{\mathrm{xx}}\) en \(\mathrm{A4}\) |
|
-3.460140 10-3 |
1 10-4 |
|
At \(t=\mathrm{0,085}\) traction - plasticity + damage phase |
||||
Membrane effort \({N}_{\mathrm{xx}}\) en \(\mathrm{A4}\) |
|
-0.069405040 |
1 10-4 |
|
At \(t=\mathrm{2,04}\) traction - discharge phase |
||||
Membrane effort \({N}_{\mathrm{xx}}\) en \(\mathrm{A4}\) |
|
-1.11050 10+5 |
1 10-4 |
|
At \(t=\mathrm{0,017}\) traction - elastic phase |
||||
Total deformation energy density in the slab in \(\mathrm{A2}\) |
|
4.642785 |
1 10-5 |
|
Membrane deformation energy density in the slab in \(\mathrm{A2}\) |
|
4.642785 |
1 10-5 |
|
Total deformation energy density in the mesh slab \(\mathrm{M1}\) |
|
4.642785 |
1 10-5 |
|
Bending strain energy density in mesh slab \(\mathrm{M1}\) |
|
0 |
1 10-13 |
|
At \(t=\mathrm{0,085}\) traction - damage phase |
||||
Total deformation energy density in the slab in \(\mathrm{A2}\) |
|
48.15097 |
1.5 10-1 |
|
Total deformation energy density in the mesh slab \(\mathrm{M1}\) |
|
48.15097 |
1.5 10-1 |
|
Bending strain energy density in mesh slab \(\mathrm{M1}\) |
|
0 |
1 10-13 |
|
At \(t=\mathrm{1,0}\) end of charge |
||||
Bending strain energy density in mesh slab \(\mathrm{M1}\) |
|
0 |
1 10-13 |
|
At \(t=\mathrm{0,017}\) traction - elastic phase |
||||
*Deformation energy in the slab |
NON_REGRESSION |
4.642785 |
1 10-5 |
|
External work |
NON_REGRESSION |
4.642785 |
1 10-5 |
|
At \(t=\mathrm{0,085}\) traction - damage phase |
||||
*Deformation energy in the slab |
NON_REGRESSION |
54.78 |
2 10-2 |
|
External work |
NON_REGRESSION |
54.78 |
2 10-2 |
|
At \(t=\mathrm{1,0}\) end of charge |
||||
*Deformation energy in the slab |
NON_REGRESSION |
817.14 |
2.5 10-3 |