7. Summaries of 3D results

7.1. Summary

In the framework of the X- FEM method, it has been shown that, without particular treatment, a mesh structure with pentahedra subjected to a non-uniform loading can present strong oscillations in contact pressures, as shown by the second curve of [Figure 7.2-1]), produced with a different formulation []), made with a different formulation [bib7], made with a different formulation [], now absorbed in Code_Aster, for which the absence of a restriction algorithm did not lead to a pivot. rubbish. The same mesh structure with hexahedra subjected to the same load does not present such oscillations (modeling A serving as a reference).

Two algorithms have been proposed that make it possible to significantly reduce these oscillations. The first (third curve of [Figure 7.2-1]) seems less accurate than the second (D modeling).

Moreover, even under uniform loading, oscillations may occur and it is essential to use an algorithm for reducing the space of pressure Lagrange multipliers (modeling E).

7.2. Comparison curves

The [Figure 7.2-1] brings together the contact pressure curves along the \(\mathit{Oy}\) axis, respectively for the hexahedral mesh (modeling A), a pentahedral mesh without a processing algorithm for the LBB, a pentahedral mesh with algorithm 1 and finally a pentahedral mesh with algorithm 1 and finally a pentahedral mesh with algorithm 2 (modeling D). We note that the oscillations for the second case are so strong that at certain points the value of the contact pressure becomes positive, which would mean that the interface has separated. Both algorithms allow a visible reduction in oscillations, and we find the reference curve obtained with the hexahedron mesh.

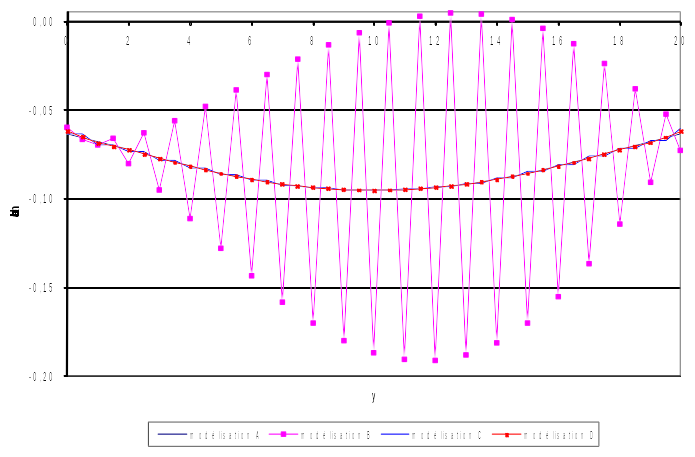
Figure 7.2-1: Comparison of contact pressures according to the models (pressures expressed in GPa)

The [Figure 7.2-2] compares the effects of the two algorithms in detail. It should be noted that the first often involves constant contact pressures in pieces, while the second tends to linearize the pressures. It is obvious that such differences are reduced by refining the mesh.

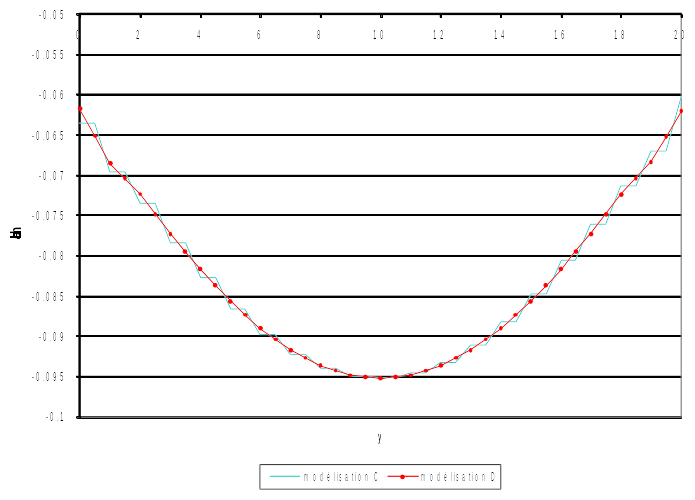
Figure 7.2-2: Comparison of the 2 algorithms (pressures expressed in GPa)