1. Reference problem#
1.1. Geometry#
The seismic response of a mass-spring system with a degree of freedom that can impact a fixed wall (problem 1) is compared to that of two identical mass-spring systems that can collide and subject to the same seismic stress (problem 2).
Problem 1 |
Problem 2 |
1.2. Material properties#
Spring stiffness: \(k=98696N/m\).
Point mass: \(m=25\mathit{kg}\).
For problem 1 (impact on a rigid wall), the normal shock stiffness is \({K}_{\mathrm{choc}}=\mathrm{5,76}{10}^{7}N/m\). As for problem 2 (shock of two deformable structures), it is worth \({K}_{\mathrm{choc}}=\mathrm{2,88}{10}^{7}N/m\).
In both cases, shock absorption is zero.
For G modeling:
Spring stiffness: \(k=500N/m\).
Point mass: \(m=15\mathit{kg}\).
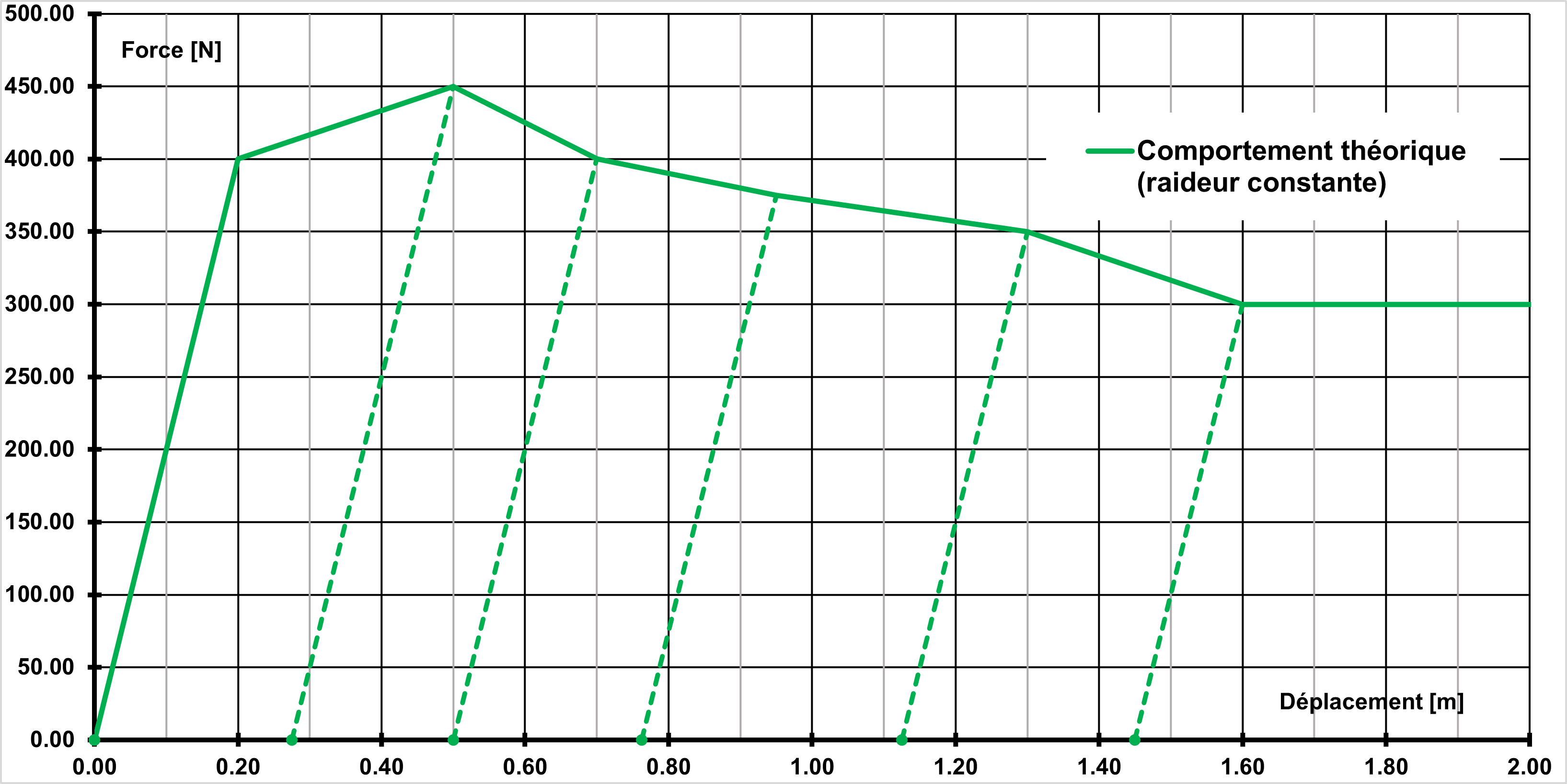
The table above gives the characteristics of material DIS_CHOC_ENDO.
The stiffness under discharge is constant, the damping is zero.
Ux [m] |
Strength [N] |
Stiffness [N/m] |
Damping [N.s/m] |
0.00 |
0.0 |
2000.0 |
0.0 |
0.20 |
400.0 |
2000.0 |
0.0 |
0.50 |
450.0 |
2000.0 |
0.0 |
0.70 |
400.0 |
2000.0 |
0.0 |
0.95 |
375.0 |
2000.0 |
0.0 |
1.30 |
350.0 |
2000.0 |
0.0 |
1.60 |
300.0 |
2000.0 |
0.0 |
20.0 |
300.0 |
2000.0 |
0.0 |
The figure below shows the behavior corresponding to the data.
1.3. Boundary conditions and loads#
Boundary conditions
The only authorized movements are translations according to axis \(x\).
Points \(A\), \(B\), and \(C\) are embedded: \(\mathrm{dx}=\mathrm{dy}=\mathrm{dz}=0\).
Loading
The anchor points \(A\) and \(B\) are subject to acceleration in the direction \(x\). Point C is subject to the opposite acceleration.
A to F models: \({\gamma }_{1}(t)=\mathrm{sin}\omega t\) with \(\omega =20.\pi {s}^{-1}\) (\({\gamma }_{2}(t)=-\mathrm{sin}\omega t\) for point C).
G modeling: \({\gamma }_{1}(t)=\alpha t\mathrm{sin}\omega t\) with \(\omega =20.\pi {s}^{-1}\) and \(\alpha =1E5\).
1.4. Initial conditions#
In both cases, the mass-spring systems are initially at rest:
to \(t=0\), \(\mathrm{dx}(0)=0\), \(\mathrm{dx}/\mathrm{dt}(0)=0\) in every way.
For problem 1, the mass is separated from the fixed wall in game \(j=5.{10}^{-4}m\). As for problem 2, the masses are separate from game \(J=2j={10}^{-3}m\).