6. Geometric stiffness - Prestressed structure#
Option: « RIGI_MECA_GE »
In the case of a prestressed structure, therefore subject to initial forces (known and independent of time), it is not possible to neglect in the equilibrium equation the terms introduced by the change in geometry from the unstressed state to the prestressed state [bib].
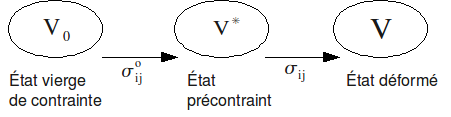
Figure 6-a : The different states.
This change in geometry changes the equilibrium equation, in the framework of the hypothesis of small disturbances (HPP) around \({V}_{o}\) (and \({V}^{\text{*}}\)), only by adding a linear term in the displacements whose associated matrix is called the geometric rigidity matrix and which is expressed by:
\({W}_{G}=\underset{{V}_{o}}{\int }\frac{\partial {u}_{k}^{\mathrm{3D}}}{\partial {x}_{i}}{\sigma }_{\text{ij}}^{o}\frac{\partial {v}_{k}^{\mathrm{3D}}}{\partial {x}_{j}}\text{dV}\)
where \({u}^{\mathrm{3D}}\) is the displacement (resp. \({v}^{\mathrm{3D}}\) the kinematically admissible virtual displacement) taken from \({V}^{\text{*}}\) (but assimilated to \({V}_{o}\) in the framework of the small disturbances hypothesis) and \({\sigma }^{o}\) the prestress (from Cauchy if you want) since we are in the framework of the hypothesis of small disturbances.
\({W}_{G}\) being a symmetric bilinear form in \({u}^{\mathrm{3D}}\) and \({v}^{\mathrm{3D}}\), it can be interpreted as the variation of a potential \({U}_{G}\).
\({W}_{G}=\delta {U}_{G}\)
We have:
\(2{U}_{G}=\underset{{V}_{o}}{\int }\frac{\partial {u}_{k}^{\mathrm{3D}}}{\partial {x}_{i}}{\sigma }_{\text{ij}}^{o}\frac{\partial {u}_{k}^{\mathrm{3D}}}{\partial {x}_{j}}\)
For a 3D beam model, the stress tensor is reduced in the local axes of the beam to components \({\sigma }_{\text{xx}}\text{,}{\sigma }_{\text{xy}}\text{et}{\sigma }_{\text{xx}}\), where:
\(2{U}_{G}=\underset{{V}_{o}}{\int }{\sigma }_{\text{xx}}^{o}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial x}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial x}+2{\sigma }_{\text{xy}}^{o}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial x}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial y}+2{\sigma }_{\text{xz}}^{o}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial x}\frac{\partial {u}_{i}^{\mathrm{3D}}}{\partial z}\)
The terms \({(\frac{\partial {u}_{x}^{\mathrm{3D}}}{\partial x})}^{2}\text{,}\frac{\partial {u}_{x}^{\mathrm{3D}}}{\partial x}\frac{\partial {u}_{x}^{\mathrm{3D}}}{\partial y}\) and \(\frac{\partial {u}_{x}^{\mathrm{3D}}}{\partial x}\frac{\partial {u}_{x}^{\mathrm{3D}}}{\partial z}\) are overlooked [bib]. In addition, in the local coordinate system of the center of torsion of the beam:
\(\{\begin{array}{}{u}_{x}^{\mathrm{3D}}(x,y,z)=u(x)+z{\theta }_{y}(x)-y{\theta }_{z}(x)\\ {u}_{y}^{\mathrm{3D}}(x,y,z)=v(x)-z{\theta }_{x}(x)\\ {u}_{z}^{\mathrm{3D}}(x,y,z)=w(x)+y{\theta }_{x}(x)\end{array}\)
and \(\nabla u=(\begin{array}{ccc}u\text{'}+z{\theta }_{y}^{\text{'}}-y{\theta }_{z}^{\text{'}}& -{\theta }_{z}& {\theta }_{y}\\ v\text{'}-z{\theta }_{x}^{\text{'}}& 0& -{\theta }_{x}\\ w\text{'}+y{\theta }_{x}^{\text{'}}& {\theta }_{x}& 0\end{array})\)
From where do we get, according to the previous hypothesis:
\(2{U}_{G}=\underset{{V}_{o}}{\int }{\sigma }_{\text{xx}}^{o}\left[{(v\text{'}-z{\theta }_{x}^{\text{'}})}^{2}+{(w\text{'}+y{\theta }_{x}^{\text{'}})}^{2}\right]+2{\sigma }_{\text{xy}}^{o}(w\text{'}+y{\theta }_{x}^{\text{'}}){\theta }_{x}+2{\sigma }_{\text{xz}}^{o}(v\text{'}-z{\theta }_{x}^{\text{'}})(-{\theta }_{x})\)
However, generalized efforts are linked to constraints by the expressions:
\(\begin{array}{ccc}{N}^{o}=\underset{S}{\int }{\sigma }_{\text{xx}}^{o}& {V}_{y}=\underset{S}{\int }{\sigma }_{\text{xy}}^{o}& {V}_{z}=\underset{S}{\int }{\sigma }_{\text{xz}}^{o}\\ & {M}_{y}=\underset{S}{\int }z{\sigma }_{\text{xx}}^{o}& {M}_{z}=\underset{S}{\int }-y{\sigma }_{\text{xx}}^{o}\end{array}\)
From this we deduce:
\(\begin{array}{}2{U}_{G}={\int }_{o}^{L}{N}^{°}({(v\text{'})}^{2}+{(w\text{'})}^{2})-2{M}_{y}^{o}v\text{'}{\theta }_{x}^{\text{'}}-2{M}_{z}^{o}w\text{'}{\theta }_{x}^{\text{'}}+2{V}_{y}^{o}w\text{'}{\theta }_{x}-2{V}_{z}^{o}v\text{'}{\theta }_{x}\\ +\underset{{V}_{o}}{\int }{\sigma }_{\text{xx}}^{o}({y}^{2}+{z}^{2}){({\theta }_{x}^{\text{'}})}^{2}+2({\sigma }_{\text{xy}}^{o}y+{\sigma }_{\text{xz}}^{o}z){\theta }_{x}{\theta }_{x}^{\text{'}}\end{array}\)
Assuming, in addition, that \({\sigma }_{\text{xx}}^{o}\) is constant in the discretized element (which is inaccurate for example for a vertical beam subject to its own weight) and that \({\theta }_{x}\) varies linearly with respect to \(x\) \({\theta }_{x}=(1-\frac{x}{L}){\theta }_{1}+\frac{x}{L}{\theta }_{2}\), where \({\theta }_{x}^{\text{'}}\text{=-}\frac{1}{L}{\theta }^{1}+\frac{1}{L}{\theta }^{2}\), it comes from:
\(\underset{{V}_{o}}{\int }{\sigma }_{\text{xx}}^{o}({y}^{2}+{z}^{2}){({\theta }_{x}^{\text{'}})}^{2}=({\theta }_{1}\text{,}{\theta }_{2})\left[\begin{array}{c}\frac{{N}^{o}}{L}\frac{{I}_{y}+{I}_{z}}{S}\text{}-\frac{{N}^{o}}{L}\text{}\frac{{I}_{y}+{I}_{z}}{S}\\ -\frac{{N}^{o}}{L}\frac{{I}_{y}+{I}_{z}}{S}\text{}\frac{{N}^{o}}{L}\text{}\frac{{I}_{y}+{I}_{z}}{S}\end{array}\right](\begin{array}{c}{\theta }_{1}\\ \\ {\theta }_{2}\end{array})\)
By neglecting in particular the terms due to the influence of the shear force on the buckling or vibration mode, and by assuming that the distributed loads are zero on an element, we have:
\(N(x)\) = constant, \({M}_{y}=({M}_{\mathrm{y2}}-{M}_{\mathrm{y1}})\frac{x}{L}+{M}_{\mathrm{y1}}\)
\({V}_{y}(x)\) = constant,
\({V}_{z}(x)\) = constant, \({M}_{z}=({M}_{\mathrm{z2}}-{M}_{\mathrm{z1}})\frac{x}{L}+{M}_{\mathrm{z1}}\)
Under this hypothesis and for the Euler-Bernoulli model (for the Timoshenko model, the same matrix is used), the following matrix is obtained:
\(A=(\begin{array}{cc}{A}_{1}& {A}_{2}\\ 0& {A}_{3}\end{array})\)
Upper triangular part of the geometric rigidity matrix with:
\({A}_{1}\) = |
1 \({u}_{1}\) |
2 \({v}_{1}\) |
3 \({w}_{1}\) |
4 \({\theta }_{\mathrm{x1}}\) |
5 \({\theta }_{\mathrm{y1}}\) |
6 \({\theta }_{\mathrm{z1}}\) |
|
1 |
|||||||
2 |
\(1.2\frac{{N}^{o}}{L}\) |
\(-\frac{{M}_{\mathrm{y1}}^{o}}{\mathrm{2L}}-\frac{{M}_{\mathrm{y2}}^{o}}{\mathrm{2L}}+\frac{{V}_{z}^{o}}{2}\) |
\(\frac{{N}^{o}}{10}\) |
||||
3 |
\(1.2\frac{{N}^{o}}{L}\) |
\(-\frac{{M}_{\mathrm{z1}}^{o}}{\mathrm{2L}}-\frac{{M}_{\mathrm{z2}}^{o}}{\mathrm{2L}}-\frac{{V}_{y}^{o}}{2}\) |
\(-\frac{{N}^{o}}{10}\) |
||||
4 |
\(\frac{({I}_{y}+{I}_{z}){N}^{o}}{(SL)}\) |
\(\frac{-{M}_{\mathrm{z1}}^{o}+{M}_{\mathrm{z2}}^{o}}{12}-\frac{L{V}_{y}^{o}}{12}\) |
\(\frac{{M}_{\mathrm{y1}}^{o}-{M}_{\mathrm{y2}}^{o}}{12}-\frac{L{V}_{z}^{o}}{12}\) |
||||
5 |
\(\frac{2L{N}^{o}}{15}\) |
||||||
6 |
\(\frac{2L{N}^{o}}{15}\) |
\({A}_{2}\) = |
7 \({u}_{2}\) |
8 \({v}_{2}\) |
9 \({w}_{2}\) |
10 \({\theta }_{\mathrm{x2}}\) |
11 \({\theta }_{\mathrm{y2}}\) |
12 \({\theta }_{\mathrm{z2}}\) |
|
1 |
|||||||
2 |
\(-1.2\frac{{N}^{o}}{L}\) |
\(\begin{array}{}\frac{{M}_{\mathrm{y1}}^{o}}{2L}+\frac{{M}_{\mathrm{y2}}^{o}}{2L}\\ +\frac{{V}_{z}^{o}}{2}\end{array}\) |
\(\frac{{N}^{o}}{10}\) |
||||
3 |
\(-1.2\frac{{N}^{o}}{L}\) |
\(\begin{array}{}\frac{{M}_{\mathrm{z1}}^{o}}{2L}+\frac{{M}_{\mathrm{z2}}^{o}}{2L}\\ -\frac{{V}_{y}^{o}}{2}\end{array}\) |
\(-\frac{{N}^{o}}{10}\) |
||||
4 |
\(\begin{array}{}\frac{{M}_{\mathrm{y1}}^{o}}{2L}+\frac{{M}_{\mathrm{y2}}^{o}}{2L}\\ -\frac{{V}_{z}^{o}}{2}\end{array}\) |
\(\begin{array}{}\frac{{M}_{\mathrm{z1}}^{o}}{2L}+\frac{{M}_{\mathrm{z2}}^{o}}{2L}\\ +\frac{{V}_{y}^{o}}{2}\end{array}\) |
\(-\frac{({I}_{y}+{I}_{z}){N}^{o}}{(SL)}\) |
\(\begin{array}{c}\frac{\left({M}_{z1}^{o}-{M}_{z2}^{o}\right)}{12}\\ +\frac{L{V}_{y}^{o}}{12}\end{array}\) |
\(\begin{array}{c}\frac{\left(-{M}_{y1}^{o}+{M}_{y2}^{o}\right)}{12}\\ +\frac{L{V}_{z}^{o}}{12}\end{array}\) |
||
5 |
\(\frac{{N}^{o}}{10}\) |
\(\begin{array}{}\frac{({M}_{\mathrm{z1}}^{o}-{M}_{\mathrm{z2}}^{o})}{12}\\ +\frac{L{V}_{y}^{o}}{12}\end{array}\) |
\(-\frac{L{N}^{o}}{30}\) |
||||
6 |
\(-\frac{{N}^{o}}{10}\) |
\(\begin{array}{}\frac{(-{M}_{\mathrm{y1}}^{o}+{M}_{\mathrm{y2}}^{o})}{12}\\ +\frac{L{V}_{y}^{o}}{12}\end{array}\) |
\(-\frac{L{N}^{o}}{30}\) |
\({A}_{3}\) = |
7 \({u}_{2}\) |
8 \({v}_{2}\) |
9 \({w}_{2}\) |
10 \({\theta }_{\mathrm{x2}}\) |
11 \({\theta }_{\mathrm{y2}}\) |
12 \({\theta }_{\mathrm{z2}}\) |
|
7 |
|||||||
8 |
\(1.2\frac{{N}^{o}}{L}\) |
\(\begin{array}{}-\frac{{M}_{\mathrm{y1}}^{o}}{2L}-\frac{{M}_{\mathrm{y2}}^{o}}{2L}\\ -\frac{{V}_{z}^{o}}{2}\end{array}\) |
\(-\frac{{N}^{o}}{10}\) |
||||
9 |
\(1.2\frac{{N}^{o}}{L}\) |
\(\begin{array}{}-\frac{{M}_{\mathrm{z1}}^{o}}{2L}-\frac{{M}_{\mathrm{z2}}^{o}}{2L}\\ +\frac{{V}_{y}^{o}}{2}\end{array}\) |
\(\frac{{N}^{o}}{10}\) |
||||
10 |
\(\frac{({I}_{y}+{I}_{z}){N}^{o}}{SL}\) |
\(\begin{array}{}\frac{(-{M}_{\mathrm{z1}}^{o}+{M}_{\mathrm{z2}}^{o})}{12}\\ -\frac{L{V}_{y}^{o}}{12}\end{array}\) |
\(\begin{array}{}\frac{({M}_{\mathrm{y1}}^{o}-{M}_{\mathrm{y2}}^{o})}{12}\\ -\frac{L{V}_{z}^{o}}{12}\end{array}\) |
||||
11 |
\(\frac{2L{N}^{o}}{15}\) |
||||||
12 |
\(\frac{2L{N}^{o}}{15}\) |
Using the equations \(\frac{\partial {M}_{y}}{\partial x}-{V}_{z}=0\) and \(\frac{\partial {M}_{z}}{\partial x}+{V}_{y}=0\), we find the programmed matrix.
In addition, in order to be able to deal with the problems of overturning thin beams, stressed essentially by bending moments and normal forces, it is necessary to add the hypothesis of moderate torsional rotations [bib], [bib].
This results in the following form of the travel field:
\(U(x,y,z)=u(x)+z({\theta }_{y}(x)+{\theta }_{x}(x){\theta }_{z}(x))-y({\theta }_{z}(x)-{\theta }_{x}(x){\theta }_{y}(x))\)
On the other hand, if the center of torsion \(C\) is not confused with the center of gravity, you should write:
\(\{\begin{array}{}V(x,y,z)=v(x,C)-(z-{z}_{C}){\theta }_{x}\\ W(x,y,z)=w(x,C)+(y-{y}_{C}){\theta }_{x}\end{array}\)
These two changes add additional terms to the geometric rigidity matrix:
The hypothesis of moderate rotations leads to the addition of the term to \({\mathrm{2U}}_{G}\):
\({\mathrm{2U}}_{G}^{1}={\int }_{0}^{L}-{M}_{z}^{o}({\theta }_{x}{\theta }_{y}){,}_{x}+{M}_{y}^{o}({\theta }_{x}{\theta }_{z}){,}_{x}+{V}_{y}^{o}{\theta }_{x}{\theta }_{y}+{V}_{z}^{o}{\theta }_{x}{\theta }_{y}\)
The terms from matrix \(A\) to be added are:
\(\begin{array}{cc}(4-5)\text{:}+\frac{{M}_{\mathrm{z1}}^{o}}{2}\text{}& (\text{10}-\text{11})\text{:}-\frac{{M}_{\mathrm{z2}}^{o}}{2}\\ (4-6)\text{:}-\frac{{M}_{\mathrm{y1}}^{o}}{2}\text{}& (\text{10}-\text{12})\text{:}+\frac{{M}_{\mathrm{y2}}^{o}}{2}\end{array}\)
With regard to the eccentricity of the center of torsion, the terms corresponding to:
\(\begin{array}{}{U}_{G}^{2}={N}^{o}{z}_{c}{\int }_{0}^{L}v\text{'}{\theta }_{x}^{\text{'}}-{N}^{o}{y}_{c}{\int }_{0}^{L}w\text{'}{\theta }_{x}^{\text{'}}-({y}_{c}{V}_{y}^{o}+{z}_{c}{V}_{z}^{o}){\int }_{0}^{L}{\theta }_{x}{\theta }_{x}^{\text{'}}\\ +({y}_{c}{M}_{z}^{o}-{z}_{c}{M}_{y}^{o}){\int }_{0}^{L}{({\theta }_{x}^{\text{'}})}^{2}\end{array}\)
In addition, you have to change the frame of reference as in [§ 5.1].