2. Introduction#
A beam is a solid generated by a surface of area \(S\) whose geometric center of inertia \(G\) describes a curve \(C\) called the mean fiber or neutral fiber. Area \(S\) is the straight section (cross section) or profile, and it is assumed that while it is evolutionary, its evolutions (size, shape) are continuous and gradual when \(G\) describes the mean line.
For the study of beams in general, the following hypotheses are made:
the straight section of the beam is undeformable,
the transverse displacement is uniform on the right section.
These hypotheses make it possible to express the displacements of any point in the section, as a function of the movements of the corresponding point located on the mean line, and as a function of an increase in displacement due to the rotation of the section around the transverse axes. The latter can be overlooked (POU_D_E) or be the subject of modeling (POU_D_T).
Discretization into « exact » beam elements is performed on a linear element with two nodes and six degrees of freedom per node. These degrees of freedom are the three translations \(u,v,w\) and the three rotations \({\theta }_{x},{\theta }_{y},{\theta }_{z}\).
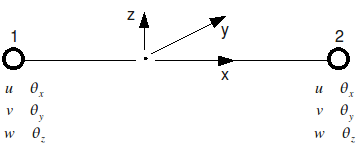
Figure 2-a: beam element and degrees of freedom.
Since the deformations are local, a local base is constructed at each vertex of the mesh, depending on the element on which we are working. The continuity of the fields of travel is ensured by a change of base, bringing the data back into the global database.
In the case of straight beams, the mean line is traditionally placed on the axis \(x\) of the local base, the transverse movements thus taking place in the plane \((y,z)\).
Finally, when we order quantities related to the degrees of freedom of an element in an elementary vector or matrix (therefore of dimension \(12\) or \({12}^{2}\)), we first order the variables for vertex 1 then those for vertex 2. For each node, we first store the quantities related to the three translations, then those related to the three rotations. For example, a displacement vector will be structured as follows: