2. Reference solution#

2.1. Calculation method used for the reference solution#

2.1.1. Pure flexure - linear work hardening#

Analytical solution:

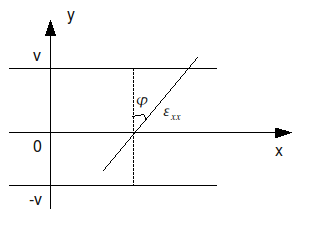
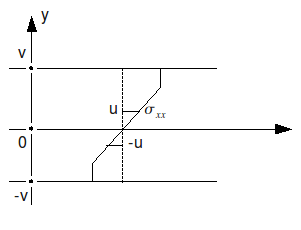
_images/1000000000000143000000E95CF50480D0B7394D.png _images/100000000000012D000000E6ED2D82D98F367544.png

\({\varepsilon }_{\mathrm{xx}}=\varphi y\) \(\varphi\): curvature

Calculation of the moment by:

\(M(u)={\int }_{s}{\sigma }_{\mathrm{xx}}(y)\mathrm{.}y\mathrm{ds}\)

\({\sigma }_{\mathrm{xx}}=E{\varepsilon }_{\mathrm{xx}}\) for \(0\le ∣y∣\le u\)

\({\sigma }_{\mathrm{xx}}={\sigma }_{y}+H({\varepsilon }_{\mathrm{xx}}-\frac{{\sigma }_{y}}{E})\)

For \(u<\mid y\mid \le v\)

We get:

for the rectangular section:

\(\frac{M}{{M}_{e}}=(1-\frac{H}{E})(\frac{3}{2}-\frac{1}{2}{(\frac{{\varphi }_{e}}{\varphi })}^{2})+\frac{H\varphi }{E}/\varphi\) with \({\varphi }_{e}=\frac{{M}_{e}}{\mathrm{EI}}{M}_{e}=\frac{{I}_{z}\cdot {\sigma }^{y}}{v}\)

for the circular section:

\(M(\mu )=\frac{{R}^{3}{\sigma }^{y}}{E}\left[\frac{\pi }{4}\frac{H}{\mu }+\frac{4}{3}(E-H){(1-{\mu }^{2})}^{3/2}+\frac{E-H}{2\mu }(\mathrm{Arc}\mathrm{sin}\mu -\mu (1-2{\mu }^{2})\sqrt{1-{\mu }^{2}})\right]\)

with \(\mu =\frac{u}{R}=\frac{{\sigma }_{y}}{\mathrm{ER}\varphi }=\frac{{\varphi }_{e}}{\varphi }\)

In discharge, after reaching the limit charge under charge, a limit charge with the opposite sign is obtained.

for the tubular section:

(Navier-Bernoulli beam hypothesis)

The limit load (\(H=0\)) is equal to:

\(\frac{M}{{M}_{e}}=\frac{4}{\pi }\)

The complete solution for a thin tube is [bib1]:

\(\frac{M(\mu )}{{M}_{e}}=\frac{\lambda }{\mu }+\frac{2(1-\lambda )}{\pi \mu }(\mathrm{arc}\mathrm{sin}\mu +\mu \sqrt{1-{\mu }^{2}})\) with \(\lambda =\frac{{E}_{T}}{E}=\frac{H}{E+H}\)

2.1.2. Traction - Linear work hardening#

Analytical solution: we immediately have \(N=S{\sigma }_{y}(1-\frac{H}{E})+\frac{\mathrm{HS}}{L}\mathrm{.}\mathrm{DX}\).

2.1.3. Pure traction - Elasticity#

Analytical solution:

\(N=\frac{\mathrm{E.S.}\delta u}{L}\) \(\sigma =\frac{\mathrm{E.}\delta u}{L}\), with \(\delta u=7.5E-03\)

2.1.4. Pure Flexion - Elasticity#

Analytical solution:

\(\mathrm{Mfz}=\frac{3.0\delta uEI}{{L}^{2}}\) \(\sigma =\frac{{M}_{\mathrm{fz}}\mathrm{.}h}{I}\), with \(\delta u=7.5E-03\)

with \(h=R\) for the circular section, \(h=v\) for the rectangular section.

2.2. Bibliographical references#

  1. J.H. LAU and T.T. LAU: Journal of Pressure Vessel Technology Vol. 106 p188-195 - May 1984.