1. Reference problem#
1.1. Geometry#
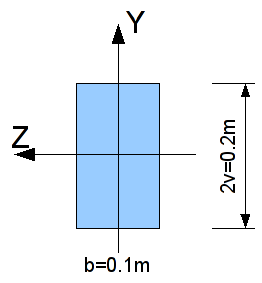
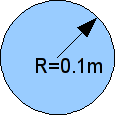
Geometric values are expressed in meters.
Straight beam of length \(L=1\), direction \(x\).
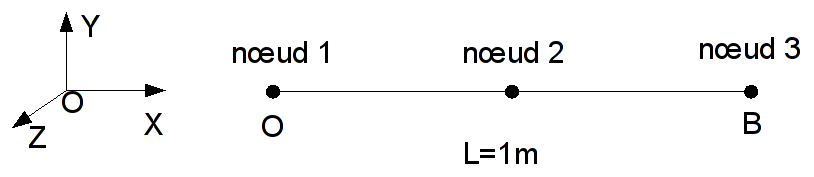
Two types of section are calculated simultaneously:
Rectangular section |
Circular section |
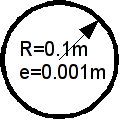
For modeling D, 1 thin tube section is calculated:
1.2. Material properties#
\(E=2.{10}^{11}\mathrm{Pa}\)
\(\nu =0.3\)
ECRO_LINE: |
\(\mathrm{SY}={\sigma }_{y}=150{10}^{6}\mathrm{Pa}\) |
\(H\) = D_ SIGM_EPSI = \(2{10}^{9}\mathrm{Pa}\) or 0 |
1.3. Boundary conditions and loads#
Embedding in \(O\)
Displacement imposed in \(B\)
\({\mathrm{DX}}^{e}=\frac{\mathrm{L.}{\sigma }_{y}}{E}={0.7510}^{-3}m\)
\(\mathrm{DX}\) varies from \({\mathrm{DX}}^{e}\) to \({\mathrm{3DX}}^{e}\)
Rotation imposed in \(B\)
\({\mathrm{DRZ}}^{e}={0.7510}^{-2}m\)
\(\mathrm{DRZ}\) varies from \({\mathrm{DRZ}}^{e}\) to \(20\mathrm{\times }{\mathit{DRZ}}^{e}\) and then decreases to \(\mathrm{-}2\mathrm{\times }{\mathit{DRZ}}^{e}\)
Note:
In pure bending, \(\mathrm{MZ}\) and \(\mathrm{DRZ}\) do not depend on \(x\). The curvature \(\varphi =\frac{d(\mathrm{DRZ})}{\mathrm{dx}}=\mathrm{DRZ}(B)\)