3. Modeling A

3.1. Characteristics of modeling

The modeling is AXIS, the contact formulation is CONTINUE, the cases with and without friction are treated.

3.2. Characteristics of the mesh

Number of knots: 743

Number of meshes and types: 671 QUAD4.

3.3. Tested sizes and results

First calculation (without friction)

Identification	Reference type	Reference value	Tolerance
\(\mathit{DY}\) at point \(M\)	“SOURCE_EXTERNE”	-0,13073410182805	0.18%
\(\mathit{SIYY}\) at point \(M\)	“SOURCE_EXTERNE”	-91.100555673515	0.09%

Second calculation (with friction)

Identification	Reference type	Reference value	Tolerance
\(\mathit{DY}\) at point \(M\)	“SOURCE_EXTERNE”	-0,12858017574262	0.18%
\(\mathit{SIYY}\) at point \(M\)	“SOURCE_EXTERNE”	-88,665240835356	0.05%

3.4. notes

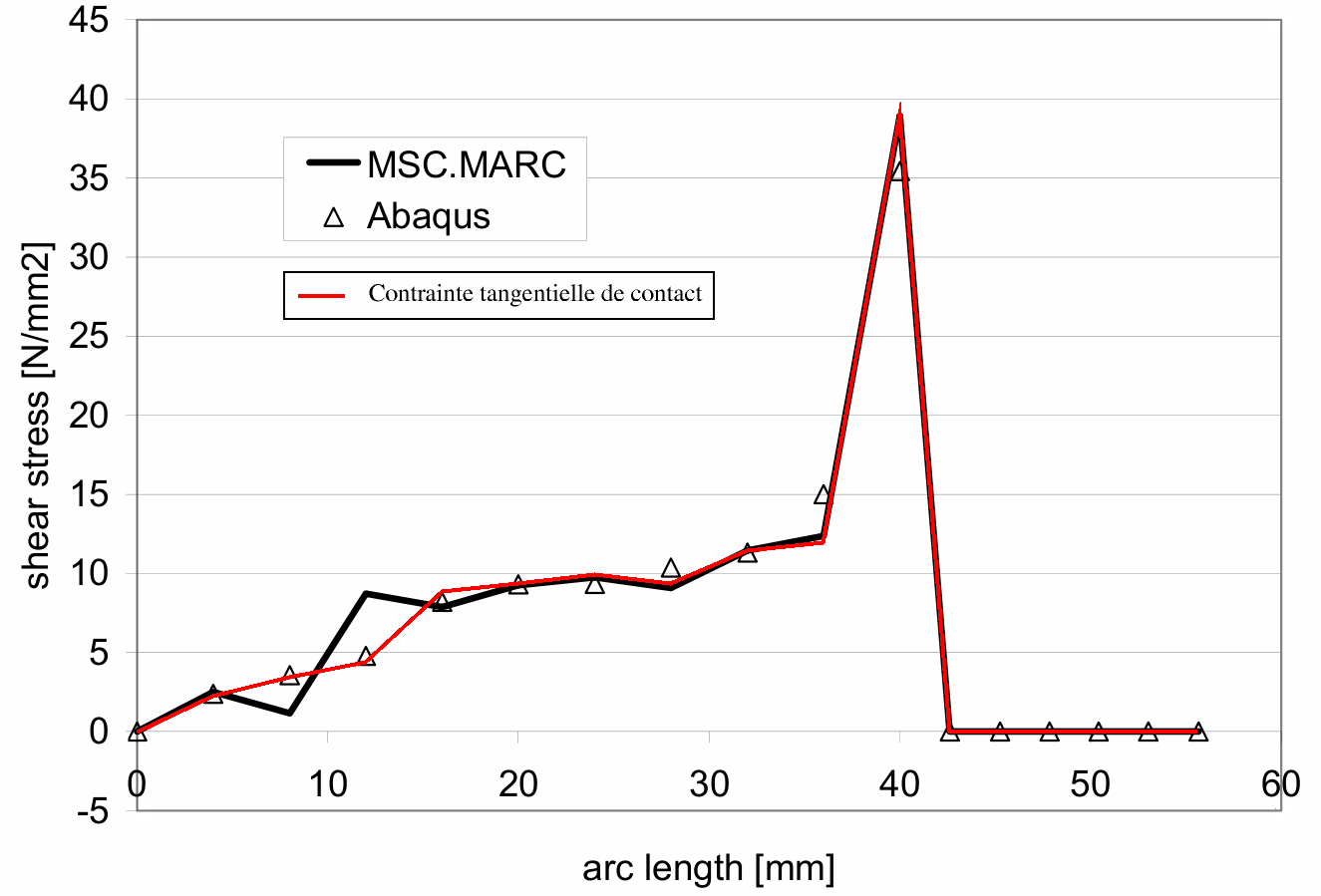
Figure 1: Comparison of tangential stress between Abaqus, MARC, and*Code_Aster*

The results obtained by the continuous formulation in Code_Aster with and without friction are in very good agreement with those of the reference codes. The figure above shows, for example, that the tangential stress on the edge in contact measured from the degree of freedom LAGS_F1 coincides with the solution of MARC.

However, it should be noted that the contact pressure given by the degree of freedom LAGS_C for the point M (located on the axis of revolution) is disturbed in continuous formulation. Indeed, the Jacobian is zero for the points on the axis of revolution. However, for linear elements, the integration diagram by default (and recommended) is of the trapezium type (therefore at the nodes).

This test illustrates the value of functionalities specific to continuous formulation that make it possible to take into account initial contact (to block rigid body movements) and to exclude knots from friction only (to avoid incompatibilities between boundary conditions and friction-contact conditions).