10. H modeling#
10.1. Characteristics of modeling#
In this modeling, it is verified that the two thermal expansion loads (homogeneous temperature in the thickness and constant temperature gradient in the thickness) lead to the same state of stress as two simple mechanical loads: extension along Ox and bending around Oy.
Note: this check is valid regardless of the behavioral relationship.
\(\mathrm{A6}\)
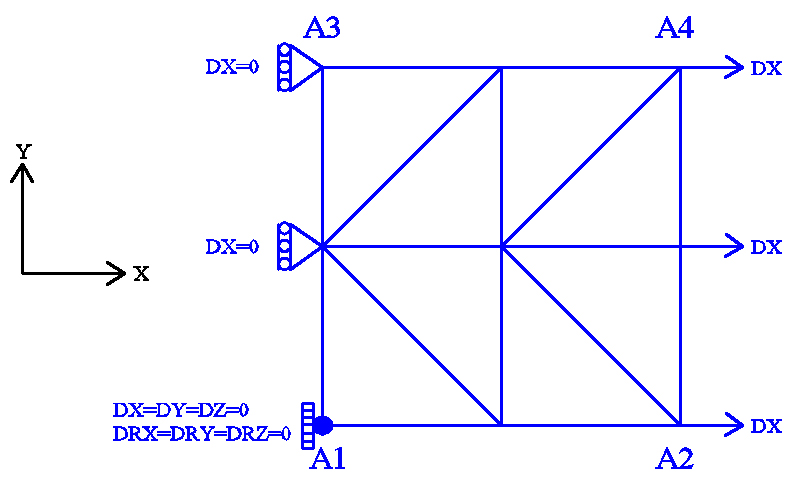
Figure 10.1-a : mesh and boundary conditions ( c load 1)
Modeling: DKT
Behavioral relationships: BETON_REGLE_PR
Boundary conditions:
Embedding in \({A}_{1}\);
\(\mathit{DX}=0.0\) on the \({A}_{1}-{A}_{3}\) edge;
\(\mathit{DRY}=0.0\) on the \({A}_{1}-{A}_{3}\) ridge
Load 1 (extension):
The reference calculation is done with the following mechanical load:
\(\mathit{DX}=2.e-4\) on the \({A}_{2}-{A}_{4}\) ridge
The equivalent thermo-mechanical load is:
\(\mathit{DX}=0.0\) on the \({A}_{2}-{A}_{4}\) ridge
Reference temperature: \(+{10}^{o}C\)
Homogeneous temperature imposed: \(\mathrm{-}{10}^{o}C\)
Coefficient of thermal expansion: \(\alpha \mathrm{=}1.e\mathrm{-}5{\mathrm{/}}^{o}C\)
Loading 2 (flexure, see modeling B):
The reference calculation is done with the following mechanical load:
\(\mathit{DRY}=6.e-3\) on the \({A}_{2}-{A}_{4}\) ridge
The equivalent thermo-mechanical load is:
\(\mathit{DRY}=0.0\) on the \({A}_{2}-{A}_{4}\) ridge
Reference temperature: \(+{10}^{o}C\)
Homogeneous temperature gradient imposed: \({T}_{\text{inf}}\mathrm{=}+{40}^{o}C,{T}_{\text{mil}}\mathrm{=}+{10}^{o}C,{T}_{\text{sup}}\mathrm{=}\mathrm{-}{20}^{o}C\)
Coefficient of thermal expansion: \(\alpha \mathrm{=}1.e\mathrm{-}5{\mathrm{/}}^{o}C\)
Reminder: the thickness of the shell is \(0.1m\)
10.2. Characteristics of the mesh#
Number of knots: 9.
Number of stitches: 8 TRIA3; 8 SEG2.
10.3. Tested quantities and results for loading 1#
For equivalent mechanical and thermal loads, it is verified that the force (homogeneous in the plate) is the same. The significant component here is NXX.
The results are very good. The thermo-mechanical loads give the same results as the equivalent mechanical loads for the behavioral relationships GLRC_DM and ENDO_ISOT_BETON (see test case ssns106o).
Identification |
Reference type |
Reference value |
Tolerance |
Effort EFGE_ELNO \(\mathit{NXX}\) for knit \(\mathit{M8}\), knot \(\mathit{N7}\) |
|
278768.0 |
1 10-3 |
10.4. Tested quantities and results for loading 2#
For equivalent mechanical and thermal loads, it is verified that the force (homogeneous in the plate) is the same. The significant component here is MXX.
The results are very good. Thermo-mechanical loads give the same results as equivalent mechanical loads for behavioral relationships GLRC_DM and ENDO_ISOT_BETON (see test case ssns106o).
Identification |
Reference type |
Reference value |
Tolerance |
Effort EFGE_ELNO \(\mathit{MXX}\) for knit \(\mathit{M8}\), knot \(\mathit{N7}\) |
|
8366.7994 |
1 10-3 |