1. Reference problem#
1.1. 3D geometry#
The structure is a straight parallelepiped with a square base. The dimensions of the bar (see []) are: \(\mathit{LX}\mathrm{=}5m\), \(\mathit{LY}\mathrm{=}5m\) and \(\mathit{LZ}\mathrm{=}25m\).
The crack (or rather the interface) is introduced by level functions (level sets) directly into the command file using the DEFI_FISS_XFEM [U4.82.08] operator. The interface is present in the middle of the structure through its representation by a level set \(\mathit{LSN}\) (see []) equation:
\(\mathrm{LSN}\) (for the interface map): \(Z\mathrm{-}\frac{\mathit{LZ}}{2}\)
Figure 1.1-b

Figure 1.1-a : Bar geometry and interface position
1.2. 2D geometry#
The structure is a rectangle. The dimensions of the bar (see []) are: \(\mathrm{LX}=1m\), \(\mathrm{LY}=5m\).
The interface is introduced by a level set function directly into the command file using the DEFI_FISS_XFEM [U4.82.08] operator. The interface is present in the middle of the structure through its representation by a level set \(\mathrm{LSN}\) (see []) equation:
\(\mathrm{LSN}\) (for the interface map): \(Y-\frac{\mathrm{LY}}{2}\)
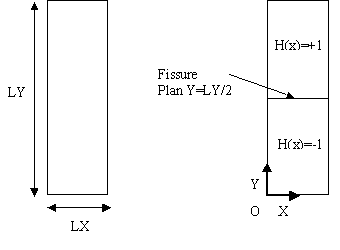
Figure 1.2-a : Plate geometry and interface position
1.3. Material properties#
Young’s module: \(E\mathrm{=}205000\mathit{MPa}\)
Poisson’s ratio: \(\nu \mathrm{=}0.3\)
1.4. Boundary conditions and loads#
The nodes on the lower face of the bar are embedded and a displacement is imposed on those on the upper face. Here we want to show the possibility of separating a finite element in two with X‑FEM.