4. C modeling#
4.1. Characteristics of the mesh and the interface#
We consider a structure with dimensions \(\mathrm{LX}=5m\), \(\mathrm{LY}=5m\), and \(\mathrm{LZ}=25m\). This structure is discretized with 5 HEXA8 meshes. We are interested in a normal flat interface
\(n=(\begin{array}{}-1\\ 1\\ 1\end{array})\)
passing through point \(A\) with coordinates \((\mathrm{5,}5\delta ,5)\). The [] shows a zoom of the 2nd element where the interface trace is represented in red.
5
N9 ROAD
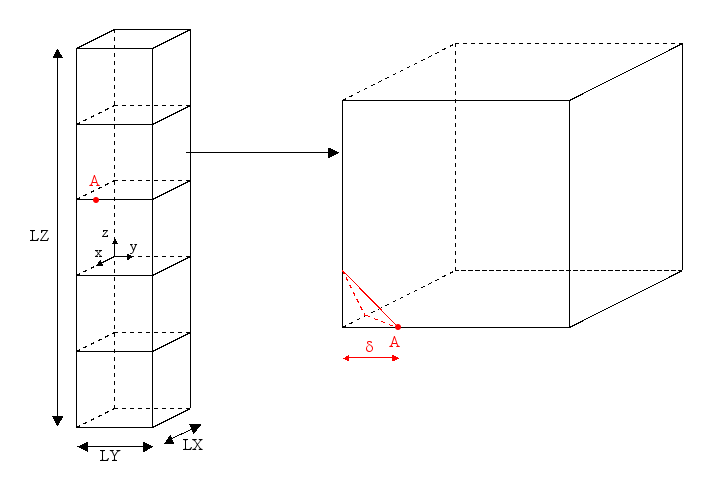
Figure 4.1-a : C mesh and zoom
The interface is characterized by the normal level set with the cartesian equation:
\(\mathrm{lsn}=-x+y+z-5\delta\)
Note:
With the new displacement jump enrichment [:ref:`R7.02.12 <R7.02.12>`], we do not see a decrease in precision on the solution when moving in the vicinity of the interface and a conditioning problem, although the interface is flat compared to the nodes of the mesh.
4.2. Boundary conditions#
The boundary conditions are the same as those in modeling B. The nodes on the lower face are embedded and a tensile displacement is imposed on the nodes on the upper face:
Lower side: \(\mathrm{DX}=0\), \(\mathrm{DY}=0\), and \(\mathrm{DZ}=0\)
Top side: \(\mathrm{DX}=0\), \(\mathrm{DY}=0\), and \(\mathrm{DZ}={10}^{-6}\)
4.3. Tested sizes and results#
The smooth running of the calculation allows a priori to validate the case. We therefore test the values of the displacement just above the interface after convergence of the iterations of the operator STAT_NON_LINE.
Identification |
Reference |
Tolerance |
\(\mathit{DZ}\) for all nodes just above the interface |
\(1.0E-6\) |
1.0E -3% |
To test all the nodes at once, we test the MINIMUM and the MAXIMUM of the column.