1. Reference problem#
1.1. Geometry#
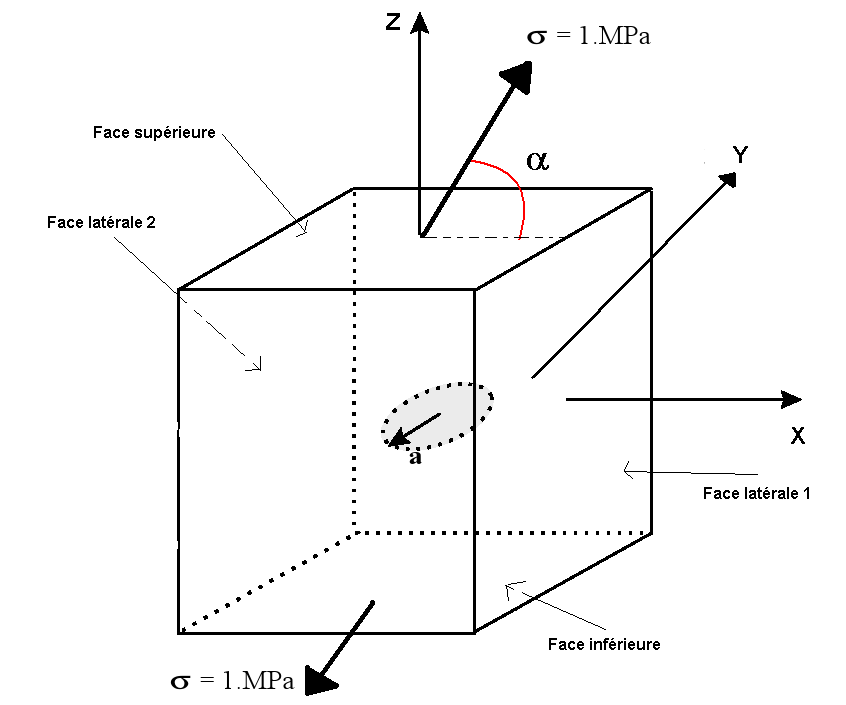
Figure 1.1-1: geometry of the cracked cube
The crack is circular (penny shaped crack) with radius \(a\mathrm{=}\mathrm{2m}\) in the \(\mathit{OXY}\) plane. The side of the cube is \(L\mathrm{=}\mathrm{10a}\) long. Thus, it is considered that the crack is in an infinite medium.
1.2. Material properties#
The material is isotropic elastic whose properties are:
\(E\mathrm{=}200000\mathrm{MPa}\)
\(\nu \mathrm{=}\mathrm{0,3}\)
1.3. Boundary conditions and loads#
Given the symmetries of the structure, the crack, and the loads, only half of the structure is modeled: half-space such as \(Y>0\). Symmetry conditions are therefore applied to the face in \(Y\mathrm{=}0\): on this face, the following movement \(Y\) is blocked.
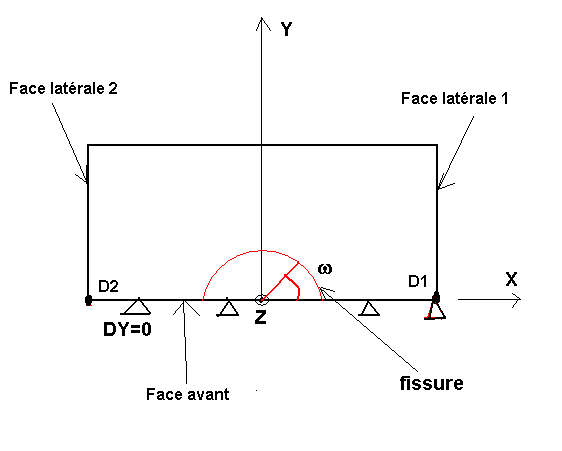
Figure 1.3-1: Symmetry condition
The structure is subject to a \({\sigma }_{\mathit{xx}}\mathrm{=}1\mathit{MPa}\) constraint. The local coordinate system \((x,y,z)\) is obtained by rotating an angle \(\alpha \mathrm{=}\pi \mathrm{/}4\) around the axis \(\mathit{OY}\).
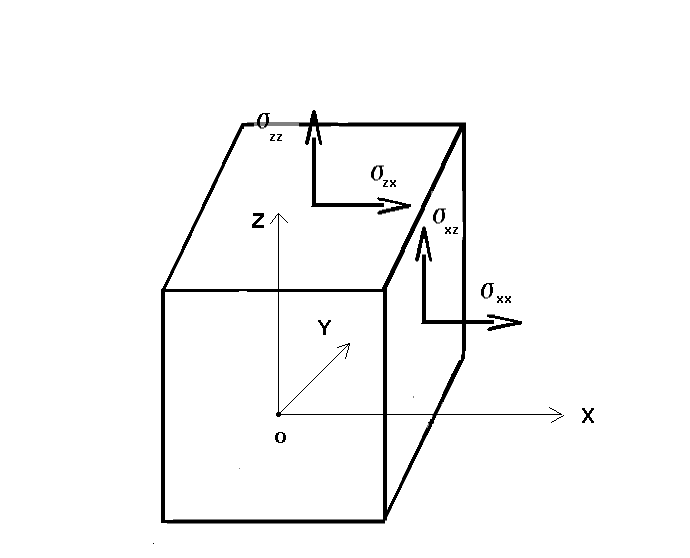
Figure 1.3-2: Constraints in the global coordinate system
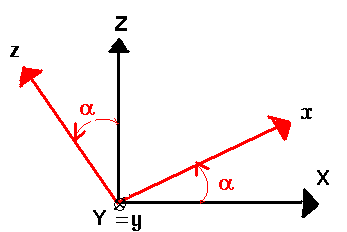
Figure 1.3-3: Local coordinate system
So, we have:
on the upper side:
\({\sigma }_{\mathit{ZZ}}\mathrm{=}\sigma {\mathrm{sin}}^{2}(\alpha )\)
\({\sigma }_{\mathit{ZX}}\mathrm{=}\sigma \mathrm{cos}(\alpha )\mathrm{sin}(\alpha )\)
on the underside:
\({\sigma }_{\mathit{ZZ}}\mathrm{=}\mathrm{-}\sigma {\mathrm{sin}}^{2}(\alpha )\)
\({\sigma }_{\mathit{ZX}}\mathrm{=}\mathrm{-}\sigma \mathrm{sin}(\alpha )\mathrm{cos}(\alpha )\)
on the right side face:
\({\sigma }_{\mathit{XX}}\mathrm{=}\sigma {\mathrm{cos}}^{2}(\alpha )\)
\({\sigma }_{\mathit{XZ}}\mathrm{=}\sigma \mathrm{cos}(\alpha )\mathrm{sin}(\alpha )\)
on the left side face:
\({\sigma }_{\mathit{XX}}\mathrm{=}\mathrm{-}\sigma {\mathrm{cos}}^{2}(\alpha )\)
\({\sigma }_{\mathit{XZ}}\mathrm{=}\sigma \mathrm{cos}(\alpha )\mathrm{sin}(\alpha )\)
In order to block rigid body modes, the point \(\mathit{D1}\) \((L\mathrm{/}\mathrm{2,0}\mathrm{,0})\) is blocked following \(X\) and \(Z\) and the point \(\mathit{D2}\) \((\mathrm{-}L\mathrm{/}\mathrm{2,0}\mathrm{,0})\) is blocked following \(Z\).
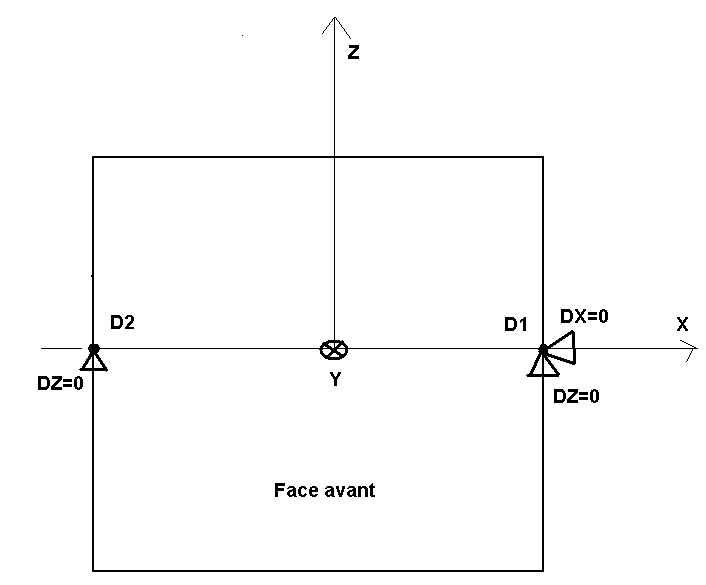
Figure 1.3-4: Blocking rigid modes