5. E modeling#

5.1. Geometry and modeling#

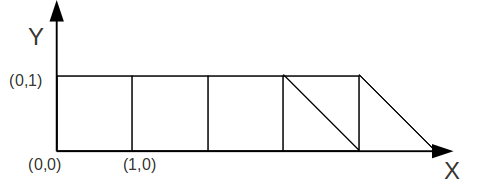
The mesh is composed of:

3 QUAD4sur meshes that affect the C_ PLAN, D_ PLANet AXIS models.
3 TRIA3sur meshes that affect the C_ PLAN, D_ PLANet AXIS models.

5.2. Orientation of the local coordinate system#

In order to define the local coordinate system for these elements, the keyword factor MASSIF from the AFFE_CARA_ELEM operator is used (see U4.42.01).

In the 2D case, the orientation of the coordinate system is taken into account by the ANGL_REP keyword, which only has one component left.

The table above gives the orientations chosen for each element:

QUAD4	ANGL_REP	\(90\)
TRIA3	ANGL_REP	\(45\)

5.3. Calculating local landmarks#

The local landmarks are formed by the vectors \(x\) and \(y\).

The values given in ANGL_REP define the following guidelines:

\(x\mathrm{=}(\mathrm{0,1})\) and \(y\mathrm{=}(\mathrm{-}\mathrm{1,0})\) for the QUAD4
\(x=\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\) and \(y=\left(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\) for the TRIA3

5.4. Tested sizes#

The tested results are shown in the following table:

MAILLE	Vector	Component	Reference Value	Tolerance
CPL4	\(x\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
CPL4	\(x\)	\(Y\)		\(1\)	\(1.E\mathrm{-}8\)
DPL4	\(x\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
DPL4	\(x\)	\(Y\)		\(1\)	\(1.E\mathrm{-}8\)
AXI4	\(x\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
AXI4	\(x\)	\(Y\)		\(1\)	\(1.E\mathrm{-}8\)
CPL3	\(x\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
CPL3	\(x\)	\(Y\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
DPL3	\(x\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
DPL3	\(x\)	\(Y\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
AXI3	\(x\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
AXI3	\(x\)	\(Y\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
CPL4	\(y\)	\(X\)		\(\mathrm{-}1\)	\(1.E\mathrm{-}8\)
CPL4	\(y\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
DPL4	\(y\)	\(Y\)		\(\mathrm{-}1\)	\(1.E\mathrm{-}8\)
DPL4	\(y\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
AXI4	\(y\)	\(Y\)		\(\mathrm{-}1\)	\(1.E\mathrm{-}8\)
AXI4	\(y\)	\(X\)		\(0\)	\(1.E\mathrm{-}8\)
CPL3	\(y\)	\(Y\)		\(\mathrm{-}0.707106781186E0\)	\(1.E\mathrm{-}8\)
CPL3	\(y\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
DPL3	\(y\)	\(Y\)		\(\mathrm{-}0.707106781186E0\)	\(1.E\mathrm{-}8\)
DPL3	\(y\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)
AXI3	\(y\)	\(Y\)		\(\mathrm{-}0.707106781186E0\)	\(1.E\mathrm{-}8\)
AXI3	\(y\)	\(X\)		\(0.707106781186E0\)	\(1.E\mathrm{-}8\)