7. Thermal characteristics

The various thermal behaviors are mutually exclusive.

7.1. Tags factor THER, THER_FO

Definition of constant linear thermal characteristics or a function defined by a concept such as a function of the parameter “INST”.

7.1.1. Operands LAMBDA/RHO_CP

LAMBDA = normal

Isotropic thermal conductivity.

RHO_CP = CP

Density heat at constant pressure (product of density and specific heat). This is the coefficient appearing in the equation:

\(\mathit{cp}\dot{T}\mathrm{-}\text{div}(\lambda \mathrm{.}\mathit{grad}T)\mathrm{=}f\)

7.2. Keyword factor THER_ORTH

Definition of thermal characteristics for an orthotropic material.

The reader may refer to the following documentation:

[U4.42.03] DEFI_COMPOSITE

[U4.42.01] AFFE_CARA_ELEM

to define the longitudinal direction associated with shells or non-isotropic 3D.

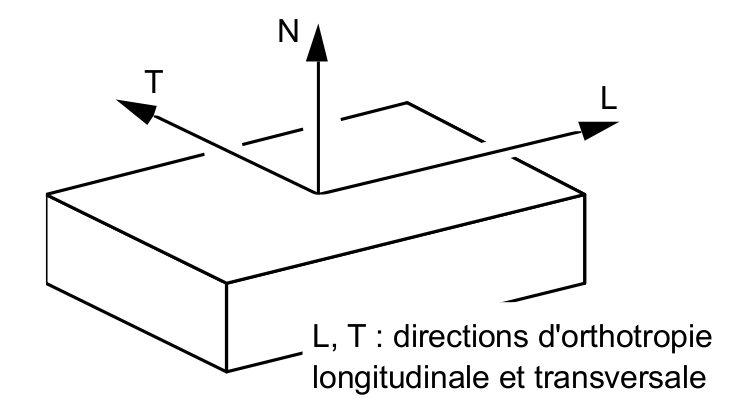
7.2.1. Operands LAMBDA/RHO_CP

LAMBDA_L = lal

Thermal conductivity in the longitudinal direction.

LAMBDA_T = lat

Thermal conductivity in the transverse direction.

LAMBDA_N = lan

Thermal conductivity in the normal sense.

RHO_CP = CP

Volume heat.

7.3. Keyword factor THER_NL

Allows you to describe thermal characteristics that depend on temperature. The formulation involves volume enthalpy (cf. [R5.02.02]).

\(\dot{\beta }-\text{div}(\lambda (T)\mathrm{.}\mathrm{grad}T)=f\)

7.3.1. Operands BETA/LAMBDA/RHO_CP

BETA = beta

Volume enthalpy as a function of temperature. For enthalpy, the extensions of the function are necessarily linear.

RHO_CP = CP

Volume heat.

If the enthalpy is not provided by the user, it will be calculated by integrating RHO_CPet will not be extended to the left. RHO_CPdoit therefore be defined over the entire calculation range which means that the extension to the left of RHO_CPest ignored for the estimation of the enthalpy.

LAMBDA = normal

Isotropic thermal conductivity as a function of temperature.

Note:

It is not possible to use a formula for these three material parameters because the algorithm needs to calculate their derivative many times, which is more easily accessible for a piecewise linear function. Thus, if the user wants to use a formula rather than a function, he must first tabulate it using the command CALC_FONC_INTERP.

7.4. Tags factor THER_COQUE, THER_COQUE_FO

Allows to define membrane and transverse conductivities and heat capacity for homogenized heterogeneous thermal shells.

The directions 1 and 2 designate those of the plane of the plate, the direction 3 is perpendicular. It is assumed that the conductivity tensor at each point is diagonal and that its eigenvalues are l1, l2 and l3. The coefficients are therefore defined by the user in the orthotropy coordinate system of the plate.

The code then changes the coordinate system to find the correct values in the element coordinate system.

7.4.1. Operands COND_LMM/COND_LMP/COND_LPP/COND_LSI//COND_TMM//COND_TMP/COND_TPP/COND_TSI

P1, P2, P3 designate the functions of interpolation of the temperature in the thickness.

If a is the mean surface conductivity matrix defined in the note [R3.11.01], then we have for the membrane conductivity tensor.

COND_LMM = a1111

term related to the integral of L1*P1*P1

COND_LMP = a1112

term related to the integral of L1*p1*p2

COND_LPP = a1122

term related to the integral of L1*p2*p2

COND_LSI = a1123

term related to the integral of L1*p2*p3

COND_TMM = a2211

term related to the integral of L2*p1*p1

COND_TMP = a2212

term related to the integral of L2*p1*p2

COND_TPP = a2222

term related to the integral of L2*p2*p2

COND_TSI = a2223

term related to the integral of L2*p2*p3

Operands COND_NMM/COND_NMP/COND_NPP/COND_NSI

If b is the tensor that describes transverse conduction and exchanges on surfaces \({\omega }_{\text{+}}\) and \({\omega }_{\text{-}}\), defined in the note [R3.11.01], we have for the transverse conductivity tensor:

COND_NMM = b11

term related to the integral of L3*p1*p1

COND_NMP = B12

term related to the integral of L3*p1*p2

COND_NPP = b22

term related to the integral of L3*p2*p2

COND_NSI = b23

term related to the integral of L3*p2*p3

7.4.2. Operands CMAS_MM/CMAS_MP/CMAS_PP/CMAS_SI

Finally, we have for the heat capacity tensor.

CMAS_MM = c11

term related to the integral of RHOCP *P1*P1

CMAS_MP = c12

term related to the integral of RHOCP *P1*P2

CMAS_PP = c22

term related to the integral of RHOCP *P2*P2

CMAS_SI = c23

term related to the integral of RHOCP *P2*P3

7.5. Keyword factor THER_NL_ORTH

Identical to THER_NL, making it possible to describe thermal characteristics dependent on temperature, this material also allows the definition of thermal characteristics for an orthotropic material, which may themselves depend on temperature.

The reader may refer to the following documentation:

[U4.42.03] DEFI_COMPOSITE

[U4.42.01] AFFE_CARA_ELEM

to define the longitudinal direction associated with shells or non-isotropic 3D.

7.5.1. Operands BETA/LAMBDA/RHO_CP

BETA = beta

Volume enthalpy as a function of temperature. For enthalpy, the extensions of the function are necessarily linear.

RHO_CP = CP

Volume heat.

If the enthalpy is not provided by the user, it will be calculated by integrating RHO_CPet will not be extended to the left. RHO_CPdoit therefore be defined over the entire calculation range which means that the extension to the left of RHO_CPest ignored for the estimation of the enthalpy.

LAMBDA_L = lal

Thermal conductivity in the longitudinal direction.

LAMBDA_T = lat

Thermal conductivity in the transverse direction.

LAMBDA_N = lan

Thermal conductivity in the normal sense.

Note:

It is not possible to use a formula for these material parameters because the algorithm needs to calculate their derivative many times, which is more easily accessible for a piecewise linear function. Thus, if the user wants to use a formula rather than a function, he must first tabulate it using the command CALC_FONC_INTERP.