12. Tag DISCRETet DISCRET_2D#

12.1. Affordable characteristics#

These keywords make it possible to assign directly to entities (meshes or nodes), which support elements such as DIS_T, DIS_TR (DISCRET) or 2D_DIS_T, 2D_DIS_TR (DISCRET_2D), rigidity, mass or dampening matrices **.

On all entities you can assign matrices corresponding to the degrees of freedom of translation \((T)\) only or to the degrees of freedom of translation and rotation \((\mathrm{TR})\). The matrices can be diagonal \((D)\) or full (symmetric or non-symmetric).

In all cases (symmetric, diagonal, complete matrices) the term numbering convention is enforced:

for symmetric matrices, only the upper triangular will be provided, with an imposed convention for the numbering of terms (see examples).
for diagonal matrices, only the terms of the diagonal will be provided, with an imposed convention for the numbering of the terms (see examples).
for non-symmetric matrices, we will provide all the terms, with an imposed convention for the numbering of the terms (see examples).

Matrixes can be assigned:

to knots or to POI1 meshes; they are then called \((N)\) nodal matrices,
to SEG2 meshes; they are then called \((L)\) link matrices.

If matrices are assigned to meshes or nodes, the element type DISCRET must first be assigned to these meshes or nodes by the AFFE_MODELE [U4.41.01] operator.

12.2. Syntax#

DISCRET and DISCRET_2D = _F (

♦ GROUP_MA = lgma, [l_gr_mesh]

◊ SYME = [“YES”| “NO”] [default]

# stiffness matrix

♦/CARA = | “K_T_D_N”| “K_TR_D_N”| “K_T_D_L”|”K_TR_D_L”,

“K_T_N”| “K_TR_N”| “K_T_L”| “K_TR_L”,

# mass matrix

/CARA = | “M_T_D_N”| “M_TR_D_N”, | “M_T_D_L”, | “M_TR_D_L”

“M_T_N”| “M_TR_N”| “M_T_L”| “M_TR_L”,

# amortization matries

/CARA = | “A_T_D_N”| “A_TR_D_N”| “A_T_D_L”|”A_TR_D_L”,

“A_T_N”| “A_TR_N”| “A_T_L”| “A_TR_L”,

♦/VALE = lva, [l_real]

◊ REPERE = [“LOCAL”, “GLOBAL”] [default]

◊ AMOR_HYST = amnh (0.0), [real (default)]

12.3. Operands#

12.3.1. Rules of use#

RIGIDITE or AMORTISSEMENT and SYME = “OUI” (by default)

CARA	CARA			DIS_* ENTITE VALE	2D_DIS_* VALE
“K_T_D_N”	“A_T_D_N”	node or POI1	3 terms	2 terms
“K_T_D_L”	“A_T_D_L”	s EG2	3 terms	2 terms
“K_TR_D_N”	“A_TR_D_N”	node or POI1	6 terms	3 terms
“K_TR_D_L”	“A_TR_D_L”	s EG2	6 terms	3 terms
“K_T_N”	“A_T_N”	node or POI1	6 terms	3 terms
“K_T_L”	“A_T_L”	s EG2	21 terms	10 terms
“K_TR_N”	“A_TR_N”	node or POI1	21 terms	6 terms
“K_TR_L”	“A_TR_L”	s EG2	78 terms	21 terms

RIGIDITE or AMORTISSEMENT and SYME = “NON”

CARA	CARA			DIS_* ENTITE VALE	2D_DIS_* VALE
“K_T_N”	“A_T_N”	node or POI1	9 terms	4 terms
“K_T_L”	“A_T_L”	s EG2	36 terms	16 terms
“K_TR_N”	“A_TR_N”	node or POI1	36 terms	9 terms
“K_TR_L”	“A_TR_L”	s EG2	144 terms	36 terms

MASSE and SYME = “OUI” (by default)

CARA	ENTITE	DIS_* VALE	2D_DIS_* VALE
“M_T_D_N”	node or POI1	1 (mass)	1 (mass)	1 (mass)
“M_TR_D_N”	node or POI1	10 (mass/inertia)	not available
“M_T_N”	node or POI1	6 (mass/inertia)	3 (mass/inertia)
“M_T_L”	s EG2	21 (mass/inertia)	10 (mass/inertia)
“M_T_D_L”	s EG2	1 (mass/inertia)	1 (mass/inertia)
“M_TR_N”	node or POI1	21 (mass/inertia)	6 (mass/inertia)
“M_TR_D_L”	s EG2	4 (mass/inertia)	4 (mass/inertia)
“M_TR_L”	s EG2	78 (mass/inertia)	21 (mass/inertia)

MASSE and SYME = “NON”

CARA	ENTITE	DIS_* VALE	2D_DIS_* VALE
“M_T_N”	node or POI1	9 (mass/inertia)	4 (mass/inertia)
“M_T_L”	SEG2	36 (mass/inertia)	16 (mass/inertia)
“M_TR_N”	node or POI1	36 (mass/inertia)	9 (mass/inertia)
“M_TR_L”	SEG2	144 (mass/inertia)	36 (mass/inertia)

12.3.2. Operands VALE#

♦/VALE = lva

In VALE we find the list of values used to define the elementary matrix of the discrete element. The size of this list depends on the type of item.

We use the keyword VALE if we want to do a standard calculation. The arguments for this keyword are real.

12.3.3. Operands K_ (stiffness matrices) or A_ (damping matrices)#

K_T_D_N/A_T_D_N and SYME = “OUI” (by default)

For a POI1 mesh or a node, in VALE, we find 3 values \({k}_{x}\), \({k}_{y}\), \({k}_{z}\) in DIS_T and 2 values \({k}_{x}\), \({k}_{y}\) in 2D_DIS_T in such as:

\(K\mathit{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{x}& 0& 0\\ 0& {k}_{y}& 0\\ 0& 0& {k}_{z}\end{array}\right]}\) \(K\mathit{ou}A=\stackrel{\begin{array}{cc}{U}_{x}& {U}_{y}\end{array}}{\left[\begin{array}{cc}{k}_{x}& 0\\ 0& {k}_{y}\end{array}\right]}\)

K_T_D_L/A_T_D_L and SYME = “OUI” (by default)

for a SEG2 mesh, \(K\) being the matrix previously defined:

\(\stackrel{\begin{array}{cc}\mathit{Noeud1}& \mathit{Noeud2}\end{array}}{\left[\begin{array}{cc}K& -K\\ -K& K\end{array}\right]}\)

so all you have to do is provide the 3 values \({k}_{x}\), \({k}_{y}\), \({k}_{z}\)

K_TR_D_N/A_TR_D_Net SYME = “OUI” (by default)

For a POI1 or knot mesh, we find in correspondence in VALE 6 values \({k}_{x}\), \({k}_{y}\), \({k}_{z}\), \({k}_{\mathrm{rx}}\), \({k}_{\mathrm{ry}}\), \({k}_{\mathrm{rz}}\) in DIS_TR or 3 values \({k}_{x}\), BELOVED in \({k}_{y}\) \({k}_{\mathrm{rz}}\) 2D_DIS_TR such as:

\(K\mathit{ou}A=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}{k}_{x}& 0& 0& 0& 0& 0\\ 0& {k}_{y}& 0& 0& 0& 0\\ 0& 0& {k}_{z}& 0& 0& 0\\ 0& 0& 0& {k}_{\mathit{rx}}& 0& 0\\ 0& 0& 0& 0& {k}_{\mathit{ry}}& 0\\ 0& 0& 0& 0& 0& {k}_{\mathit{rz}}\end{array}\right]}\) \(K\mathit{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{x}& 0& 0\\ 0& {k}_{y}& 0\\ 0& 0& {k}_{\mathit{rz}}\end{array}\right]}\)

K_TR_D_L/A_TR_D_L and SYME = “OUI” (by default)

for a SEG2 mesh, \(K\) being the matrix previously defined:

\(\stackrel{\begin{array}{cc}\mathit{Noeud1}& \mathit{Noeud2}\end{array}}{\left[\begin{array}{cc}K& -K\\ -K& K\end{array}\right]}\)

All you have to do is give the 6 values above.

K_T_N/A_T_N and SYME = “OUI” (by default)

for a POI1 mesh or a node, we find 6 values \({k}_{1}\), \({k}_{2}\)… \({k}_{6}\) in DIS_T or 3 values \({k}_{1}\), \({k}_{2}\), \({k}_{3}\) in VALE in such as: 2D_DIS_T

\(K\mathit{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{1}& {k}_{2}& {k}_{4}\\ & {k}_{3}& {k}_{5}\\ & & {k}_{6}\end{array}\right]}\) \(K\mathit{ou}A=\stackrel{\begin{array}{cc}{U}_{x}& {U}_{y}\end{array}}{\left[\begin{array}{cc}{k}_{1}& {k}_{2}\\ & {k}_{3}\end{array}\right]}\)

K_T_N/A_T_N and SYME = “NON”

for a POI1 mesh or a node, we find 9 values \({k}_{1}\), \({k}_{2}\)… \({k}_{9}\) in DIS_T or 4 values \({k}_{1}\), \({k}_{2}\),… \({k}_{4}\) in VALE in such as: 2D_DIS_T

\(K\mathrm{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{1}& {k}_{4}& {k}_{7}\\ {k}_{2}& {k}_{5}& {k}_{8}\\ {k}_{3}& {k}_{6}& {k}_{9}\end{array}\right]}\) \(K\mathrm{ou}A=\stackrel{\begin{array}{cc}{U}_{x}& {U}_{y}\end{array}}{\left[\begin{array}{cc}{k}_{1}& {k}_{3}\\ {k}_{2}& {k}_{4}\end{array}\right]}\)

K_T_L/A_T_L and SYME = “OUI” (by default)

for a SEG2 mesh, we find in correspondence in VALE 21 values \({k}_{1}\), \({k}_{2}\)… \({k}_{21}\) in DIS_T or 10 values \({k}_{1}\), \({k}_{2}\)… \({k}_{10}\) in 2D_DIS_T and the following stiffness matrix will be affected:

\(K\mathrm{ou}A=\stackrel{\begin{array}{cccccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{z1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}& {U}_{\mathrm{z2}}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{2}& {k}_{4}& {k}_{7}& {k}_{11}& {k}_{16}\\ & {k}_{3}& {k}_{5}& {k}_{8}& {k}_{12}& {k}_{17}\\ & & {k}_{6}& {k}_{9}& {k}_{13}& {k}_{18}\\ & & & {k}_{10}& {k}_{14}& {k}_{19}\\ & & & & {k}_{15}& {k}_{20}\\ & & & & & {k}_{21}\end{array}\right]}\) \(K\mathrm{ou}A=\stackrel{\begin{array}{cccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}\end{array}}{\left[\begin{array}{cccc}{k}_{1}& {k}_{2}& {k}_{4}& {k}_{7}\\ & {k}_{3}& {k}_{5}& {k}_{8}\\ & & {k}_{6}& {k}_{9}\\ & & & {k}_{10}\end{array}\right]}\)

K_T_L/A_T_L and SYME = “NON”

for a SEG2 mesh, in correspondence VALE, we find 36 values \({k}_{1}\), \({k}_{2}\)… \({k}_{36}\) in DIS_T or 16 values \({k}_{1}\), \({k}_{2}\)… \({k}_{16}\) in 2D_DIS_T and the following stiffness matrix will be affected:

\(K\mathrm{ou}A=\stackrel{\begin{array}{cccccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{z1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}& {U}_{\mathrm{z2}}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{2}& {k}_{4}& {k}_{7}& {k}_{11}& {k}_{16}\\ & {k}_{3}& {k}_{5}& {k}_{8}& {k}_{12}& {k}_{17}\\ & & {k}_{6}& {k}_{9}& {k}_{13}& {k}_{18}\\ & & & {k}_{10}& {k}_{14}& {k}_{19}\\ & & & & {k}_{15}& {k}_{20}\\ & & & & & {k}_{21}\end{array}\right]}\) \(K\mathrm{ou}A=\stackrel{\begin{array}{cccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}\end{array}}{\left[\begin{array}{cccc}{k}_{1}& {k}_{5}& {k}_{9}& {k}_{13}\\ {k}_{2}& {k}_{6}& {k}_{10}& {k}_{14}\\ {k}_{3}& {k}_{7}& {k}_{11}& {k}_{15}\\ {k}_{4}& {k}_{8}& {k}_{12}& {k}_{16}\end{array}\right]}\)

K_TR_N/A_TR_N and SYME = “OUI” (by default)

for a POI1 mesh or a node, we find 21 values \({k}_{1}\), \({k}_{2}\)… in correspondence in VALE \({k}_{21}\) in DIS_TR or 6 values \({k}_{1}\), \({k}_{2}\)… \({k}_{6}\) in 2D_DIS_TR such as:

\(K\mathrm{ou}A=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{2}& {k}_{4}& {k}_{7}& {k}_{11}& {k}_{16}\\ & {k}_{3}& {k}_{5}& {k}_{8}& {k}_{12}& {k}_{17}\\ & & {k}_{6}& {k}_{9}& {k}_{13}& {k}_{18}\\ & & & {k}_{10}& {k}_{14}& {k}_{19}\\ & & & & {k}_{15}& {k}_{20}\\ & & & & & {k}_{21}\end{array}\right]}\) \(K\mathrm{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{1}& {k}_{2}& {k}_{4}\\ & {k}_{3}& {k}_{5}\\ & & {k}_{6}\end{array}\right]}\)

K_TR_N/A_TR_N and SYME = “NON”

For a POI1 mesh or a node, VALE contains 36 values \({k}_{1}\), \({k}_{2}\)… \({k}_{36}\) in DIS_TR or 9 values \({k}_{1}\), \({k}_{2}\)… \({k}_{9}\) in 2D_DIS_TR such as:

\(K\mathrm{ou}A=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{7}& {k}_{13}& {k}_{19}& {k}_{25}& {k}_{31}\\ {k}_{2}& {k}_{8}& {k}_{14}& {k}_{20}& {k}_{26}& {k}_{32}\\ {k}_{3}& {k}_{9}& {k}_{15}& {k}_{21}& {k}_{27}& {k}_{33}\\ {k}_{4}& {k}_{10}& {k}_{16}& {k}_{22}& {k}_{28}& {k}_{34}\\ {k}_{5}& {k}_{11}& {k}_{17}& {k}_{23}& {k}_{29}& {k}_{35}\\ {k}_{6}& {k}_{12}& {k}_{18}& {k}_{24}& {k}_{30}& {k}_{36}\end{array}\right]}\) \(K\mathrm{ou}A=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{ccc}{k}_{1}& {k}_{4}& {k}_{7}\\ {k}_{2}& {k}_{5}& {k}_{8}\\ {k}_{3}& {k}_{6}& {k}_{9}\end{array}\right]}\)

K_TR_L/A_TR_Let SYME = “OUI” (by default)

for a SEG2 mesh, we find in correspondence in VALE 78 values \({k}_{1}\), \({k}_{2}\)… \({k}_{78}\) in DIS_TR.

or 21 values \({k}_{1}\), \({k}_{2}\)… \({k}_{21}\) in 2D_DIS_TR such as:

\(K\mathit{ou}A=\stackrel{\begin{array}{cccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{2}& {k}_{4}& {k}_{7}& {k}_{11}& {k}_{16}\\ & {k}_{3}& {k}_{5}& {k}_{8}& {k}_{12}& {k}_{17}\\ & & {k}_{6}& {k}_{9}& {k}_{13}& {k}_{18}\\ & & & {k}_{10}& {k}_{14}& {k}_{19}\\ & & & & {k}_{15}& {k}_{20}\\ & & & & & {k}_{21}\end{array}\right]}\)

K_TR_L/A_TR_Let SYME = “NON”

for a SEG2 mesh, we find in correspondence in VALE 144 values \({k}_{1}\), \({k}_{2}\)… \({k}_{144}\) in DIS_TR.

\(K\mathit{ou}A=\stackrel{\begin{array}{cccccccccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {U}_{\mathit{z1}}& {R}_{\mathit{x1}}& {R}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {U}_{\mathit{z2}}& {R}_{\mathit{x2}}& {R}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccccccccc}{k}_{1}& {k}_{13}& {k}_{25}& {k}_{37}& {k}_{49}& {k}_{61}& {k}_{73}& {k}_{85}& {k}_{97}& {k}_{109}& {k}_{121}& {k}_{133}\\ {k}_{2}& {k}_{14}& {k}_{26}& {k}_{38}& {k}_{50}& {k}_{62}& {k}_{74}& {k}_{86}& {k}_{98}& {k}_{110}& {k}_{122}& {k}_{134}\\ {k}_{3}& {k}_{15}& {k}_{27}& {k}_{39}& {k}_{51}& {k}_{63}& {k}_{75}& {k}_{87}& {k}_{99}& {k}_{111}& {k}_{123}& {k}_{135}\\ {k}_{4}& {k}_{16}& {k}_{28}& {k}_{40}& {k}_{52}& {k}_{64}& {k}_{76}& {k}_{88}& {k}_{100}& {k}_{112}& {k}_{124}& {k}_{136}\\ {k}_{5}& {k}_{17}& {k}_{29}& {k}_{41}& {k}_{53}& {k}_{65}& {k}_{77}& {k}_{89}& {k}_{101}& {k}_{113}& {k}_{125}& {k}_{137}\\ {k}_{6}& {k}_{18}& {k}_{30}& {k}_{42}& {k}_{54}& {k}_{66}& {k}_{78}& {k}_{90}& {k}_{102}& {k}_{114}& {k}_{126}& {k}_{138}\\ {k}_{7}& {k}_{19}& {k}_{31}& {k}_{43}& {k}_{55}& {k}_{67}& {k}_{79}& {k}_{91}& {k}_{103}& {k}_{115}& {k}_{127}& {k}_{139}\\ {k}_{8}& {k}_{20}& {k}_{32}& {k}_{44}& {k}_{56}& {k}_{68}& {k}_{80}& {k}_{92}& {k}_{104}& {k}_{116}& {k}_{128}& {k}_{140}\\ {k}_{9}& {k}_{21}& {k}_{33}& {k}_{45}& {k}_{57}& {k}_{69}& {k}_{81}& {k}_{93}& {k}_{105}& {k}_{117}& {k}_{129}& {k}_{141}\\ {k}_{10}& {k}_{22}& {k}_{34}& {k}_{46}& {k}_{58}& {k}_{70}& {k}_{82}& {k}_{94}& {k}_{106}& {k}_{118}& {k}_{130}& {k}_{142}\\ {k}_{11}& {k}_{23}& {k}_{35}& {k}_{47}& {k}_{59}& {k}_{71}& {k}_{83}& {k}_{95}& {k}_{107}& {k}_{119}& {k}_{131}& {k}_{143}\\ {k}_{12}& {k}_{24}& {k}_{36}& {k}_{48}& {k}_{60}& {k}_{72}& {k}_{84}& {k}_{96}& {k}_{108}& {k}_{120}& {k}_{132}& {k}_{144}\end{array}\right]}\)

or 36 values \({k}_{1}\), \({k}_{2}\)… \({k}_{36}\) in 2D_DIS_TR such as:

\(K\mathit{ou}A=\stackrel{\begin{array}{cccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccc}{k}_{1}& {k}_{7}& {k}_{13}& {k}_{19}& {k}_{25}& {k}_{31}\\ {k}_{2}& {k}_{8}& {k}_{14}& {k}_{20}& {k}_{26}& {k}_{32}\\ {k}_{3}& {k}_{9}& {k}_{15}& {k}_{21}& {k}_{27}& {k}_{33}\\ {k}_{4}& {k}_{10}& {k}_{16}& {k}_{22}& {k}_{28}& {k}_{34}\\ {k}_{5}& {k}_{11}& {k}_{17}& {k}_{23}& {k}_{29}& {k}_{35}\\ {k}_{6}& {k}_{12}& {k}_{18}& {k}_{24}& {k}_{30}& {k}_{36}\end{array}\right]}\)

12.3.4. Operands `M_*` Mass matrices#

M_T_D_N and SYME = “OUI” (by default)

For a POI1 mesh or a node, VALE has a corresponding value of \(m\). The following mass matrix will be affected:

\(M=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}m& 0& 0\\ 0& m& 0\\ 0& 0& m\end{array}\right]}\)

M_TR_D_Net SYME = “OUI” (value by default, not available in 2D_DIS_TR)

For a POI1 cell or a node, VALE has a corresponding mass value \(m\), 6 values of the inertia tensor (mass): \({I}_{\mathit{xx}},{I}_{\mathit{yy}},{I}_{\mathit{zz}},{I}_{\mathit{xy}},{I}_{\mathit{yz}},{I}_{\mathit{xz}}\) and 3 components of the mass eccentricity vector with respect to its node: \({e}_{x},{e}_{y},{e}_{z}\). The following mass matrix will be affected:

\(M=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}m& 0& 0& 0& {\mathit{m.e}}_{z}& -{\mathit{m.e}}_{y}\\ & m& 0& -{\mathit{m.e}}_{z}& 0& {\mathit{m.e}}_{x}\\ & & m& {\mathit{m.e}}_{y}& -{\mathit{m.e}}_{x}& 0\\ & & & {V}_{\mathit{xx}}& {V}_{\mathit{xy}}& {V}_{\mathit{xz}}\\ & & & & {V}_{\mathit{yy}}& {V}_{\mathit{yz}}\\ & & & & & {v}_{\mathit{zz}}\end{array}\right]}\) \(\begin{array}{c}{V}_{\mathit{xx}}={I}_{\mathit{xx}}+m({e}_{y}^{2}+{e}_{z}^{2})\\ {V}_{\mathit{yy}}={I}_{\mathit{yy}}+m({e}_{x}^{2}+{e}_{z}^{2})\\ {V}_{\mathit{zz}}={I}_{\mathit{zz}}+m({e}_{x}^{2}+{e}_{y}^{2})\\ {V}_{\mathit{xy}}={I}_{\mathit{xy}}-m{e}_{x}{e}_{y}\\ {V}_{\mathit{yz}}={I}_{\mathit{yz}}-m{e}_{y}{e}_{z}\\ {V}_{\mathit{xz}}={I}_{\mathit{xz}}-m{e}_{x}{e}_{z}\\ \end{array}\)

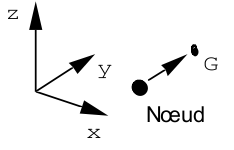
Attention:

The eccentricity must be expressed in the global coordinate system: vector coordinates \(\mathrm{NG}\) (eccentricity) directed from the node to the mass.

M_T_N and SYME = “OUI” (by default)

for a POI1 or node mesh, we find in correspondence in VALE 6 values \({M}_{1}\), \({M}_{2}\),… \({M}_{6}\) in DIS_T or 3 values \({M}_{1}\), \({M}_{2}\), \({M}_{3}\) in 2D_DIS_T and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}{M}_{1}& {M}_{2}& {M}_{4}\\ & {M}_{3}& {M}_{5}\\ & & {M}_{6}\end{array}\right]}\) \(M=\stackrel{\begin{array}{cc}{U}_{x}& {U}_{y}\end{array}}{\left[\begin{array}{cc}{M}_{1}& {M}_{2}\\ & {M}_{3}\end{array}\right]}\)

For example, see test SDLD27 [V2.01.027].

M_T_N and SYME = “NON”

for a POI1 or knot mesh, in correspondence VALE, we find 9 values \({M}_{1}\), \({M}_{2}\),… \({M}_{9}\) in DIS_T or 4 values \({M}_{1}\), \({M}_{2}\),… \({M}_{4}\) in 2D_DIS_T and the following mass matrix will be affected:

\(M=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {U}_{z}\end{array}}{\left[\begin{array}{ccc}{M}_{1}& {M}_{4}& {M}_{7}\\ {M}_{2}& {M}_{5}& {M}_{8}\\ {M}_{3}& {M}_{6}& {M}_{9}\end{array}\right]}\) \(M=\stackrel{\begin{array}{cc}{U}_{x}& {U}_{y}\end{array}}{\left[\begin{array}{cc}{M}_{1}& {M}_{3}\\ {M}_{2}& {M}_{4}\end{array}\right]}\)

M_TR_N and SYME = “OUI” (by default)

for a POI1 or node mesh, we find in correspondence in VALE 21 values \({M}_{1}\), \({M}_{2}\),… \({M}_{21}\) in DIS_TR or 6 values \({M}_{1}\), \({M}_{2}\),… \({M}_{6}\) in 2D_DIS_TR and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{2}& {M}_{4}& {M}_{7}& {M}_{11}& {M}_{16}\\ & {M}_{3}& {M}_{5}& {M}_{8}& {M}_{12}& {M}_{17}\\ & & {M}_{6}& {M}_{9}& {M}_{13}& {M}_{18}\\ & & & {M}_{10}& {M}_{14}& {M}_{19}\\ & & & & {M}_{15}& {M}_{20}\\ & & & & & {M}_{21}\end{array}\right]}\) \(M=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{ccc}{M}_{1}& {M}_{2}& {M}_{4}\\ & {M}_{3}& {M}_{5}\\ & & {M}_{6}\end{array}\right]}\)

M_TR_N and SYME = “NON”

for a POI1 or node mesh, we find in correspondence in VALE 36 values \({M}_{1}\), \({M}_{2}\),… \({M}_{36}\) in DIS_TR or 9 values \({M}_{1}\), \({M}_{2}\),… \({M}_{9}\) in 2D_DIS_TR and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cccccc}{U}_{x}& {U}_{y}& {U}_{z}& {R}_{x}& {R}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{7}& {M}_{13}& {M}_{19}& {M}_{25}& {M}_{31}\\ {M}_{2}& {M}_{8}& {M}_{14}& {M}_{20}& {M}_{26}& {M}_{32}\\ {M}_{3}& {M}_{9}& {M}_{15}& {M}_{21}& {M}_{27}& {M}_{33}\\ {M}_{4}& {M}_{10}& {M}_{16}& {M}_{22}& {M}_{28}& {M}_{34}\\ {M}_{5}& {M}_{11}& {M}_{17}& {M}_{23}& {M}_{29}& {M}_{35}\\ {M}_{6}& {M}_{12}& {M}_{18}& {M}_{24}& {M}_{30}& {M}_{36}\end{array}\right]}\) \(M=\stackrel{\begin{array}{ccc}{U}_{x}& {U}_{y}& {R}_{z}\end{array}}{\left[\begin{array}{ccc}{M}_{1}& {M}_{4}& {M}_{7}\\ {M}_{2}& {M}_{5}& {M}_{8}\\ {M}_{3}& {M}_{6}& {M}_{9}\end{array}\right]}\)

M_T_L and SYME = “OUI” (by default)

for a SEG2 mesh, we find in correspondence in VALE 21 values \({M}_{1}\), \({M}_{2}\),… \({M}_{21}\) in DIS_T or 10 values \({M}_{1}\), \({M}_{2}\),… \({M}_{10}\) in 2D_DIS_T and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cccccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{z1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}& {U}_{\mathrm{z2}}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{2}& {M}_{4}& {M}_{7}& {M}_{11}& {M}_{16}\\ & {M}_{3}& {M}_{5}& {M}_{8}& {M}_{12}& {M}_{17}\\ & & {M}_{6}& {M}_{9}& {M}_{13}& {M}_{18}\\ & & & {M}_{10}& {M}_{14}& {M}_{19}\\ & & & & {M}_{15}& {M}_{20}\\ & & & & & {M}_{21}\end{array}\right]}\) \(M=\stackrel{\begin{array}{cccc}{U}_{\mathrm{x1}}& {U}_{\mathrm{y1}}& {U}_{\mathrm{x2}}& {U}_{\mathrm{y2}}\end{array}}{\left[\begin{array}{cccc}{M}_{1}& {M}_{2}& {M}_{4}& {M}_{7}\\ & {M}_{3}& {M}_{5}& {M}_{8}\\ & & {M}_{6}& {M}_{9}\\ & & & {M}_{10}\end{array}\right]}\)

M_T_D_L and SYME = “OUI” (by default)

for a SEG2 mesh, we find 1 value in VALE, in correspondence, in, in DIS_T and in 2_DIS_T, the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cc}\mathrm{Noeud1}& \mathrm{Noeud2}\end{array}}{\left[\begin{array}{cc}M& \\ & M\end{array}\right]}\) the \(M\) matrix has the same definition as that given for the M_T_D_N.

M_T_L and SYME = “NON”

for a SEG2 mesh, we find in correspondence in VALE 36 values \({M}_{1}\), \({M}_{2}\),… \({M}_{36}\) in DIS_T or 16 values \({M}_{1}\), \({M}_{2}\),… \({M}_{16}\) in 2D_DIS_T and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {U}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {U}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{7}& {M}_{13}& {M}_{19}& {M}_{25}& {M}_{31}\\ {M}_{2}& {M}_{8}& {M}_{14}& {M}_{20}& {M}_{26}& {M}_{32}\\ {M}_{3}& {M}_{9}& {M}_{15}& {M}_{21}& {M}_{27}& {M}_{33}\\ {M}_{4}& {M}_{10}& {M}_{16}& {M}_{22}& {M}_{28}& {M}_{34}\\ {M}_{5}& {M}_{11}& {M}_{17}& {M}_{23}& {M}_{29}& {M}_{35}\\ {M}_{6}& {M}_{12}& {M}_{18}& {M}_{24}& {M}_{30}& {M}_{36}\end{array}\right]}\) \(M=\stackrel{\begin{array}{cccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}\end{array}}{\left[\begin{array}{cccc}{M}_{1}& {M}_{5}& {M}_{9}& {M}_{13}\\ {M}_{2}& {M}_{6}& {M}_{10}& {M}_{14}\\ {M}_{3}& {M}_{7}& {M}_{11}& {M}_{15}\\ {M}_{4}& {M}_{8}& {M}_{12}& {M}_{16}\end{array}\right]}\)

M_TR_L and SYME = “OUI” (by default)

for a SEG2 mesh, we find in correspondence in VALE 78 values \({M}_{1}\), \({M}_{2}\),… \({M}_{78}\) in DIS_TR and the following mass matrix will be assigned:

or 21 values \({M}_{1}\), \({M}_{2}\),… \({M}_{21}\) in 2D_DIS_TR

\(M=\stackrel{\begin{array}{cccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{2}& {M}_{4}& {M}_{7}& {M}_{11}& {M}_{16}\\ & {M}_{3}& {M}_{5}& {M}_{8}& {M}_{12}& {M}_{17}\\ & & {M}_{6}& {M}_{9}& {M}_{13}& {M}_{18}\\ & & & {M}_{10}& {M}_{14}& {M}_{19}\\ & & & & {M}_{15}& {M}_{20}\\ & & & & & {M}_{21}\end{array}\right]}\)

M_TR_D_Let SYME = “OUI” (by default)

for a SEG2 mesh, in correspondence VALE, we find 4 values \(\mathit{M1}\), \(\mathit{M2}\),… \(\mathit{M4}\) in DIS_TR and the following mass matrix will be assigned:

or 2 values \(\mathit{M1}\), \(\mathit{M2}\) and 2D_DIS_TR

M_TR_L and SYME = “NON”

for a SEG2 mesh, we find in correspondence in VALE 144 values \({M}_{1}\), \({M}_{2}\),… \({M}_{144}\) in DIS_TR and the following mass matrix will be assigned:

\(M=\stackrel{\begin{array}{cccccccccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {U}_{\mathit{z1}}& {R}_{\mathit{x1}}& {R}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {U}_{\mathit{z2}}& {R}_{\mathit{x2}}& {R}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccccccccc}{M}_{1}& {M}_{13}& {M}_{25}& {M}_{37}& {M}_{49}& {M}_{61}& {M}_{73}& {M}_{85}& {M}_{97}& {M}_{109}& {M}_{121}& {M}_{133}\\ {M}_{2}& {M}_{14}& {M}_{26}& {M}_{38}& {M}_{50}& {M}_{62}& {M}_{74}& {M}_{86}& {M}_{98}& {M}_{110}& {M}_{122}& {M}_{134}\\ {M}_{3}& {M}_{15}& {M}_{27}& {M}_{39}& {M}_{51}& {M}_{63}& {M}_{75}& {M}_{87}& {M}_{99}& {M}_{111}& {M}_{123}& {M}_{135}\\ {M}_{4}& {M}_{16}& {M}_{28}& {M}_{40}& {M}_{52}& {M}_{64}& {M}_{76}& {M}_{88}& {M}_{100}& {M}_{112}& {M}_{124}& {M}_{136}\\ {M}_{5}& {M}_{17}& {M}_{29}& {M}_{41}& {M}_{53}& {M}_{65}& {M}_{77}& {M}_{89}& {M}_{101}& {M}_{113}& {M}_{125}& {M}_{137}\\ {M}_{6}& {M}_{18}& {M}_{30}& {M}_{42}& {M}_{54}& {M}_{66}& {M}_{78}& {M}_{90}& {M}_{102}& {M}_{114}& {M}_{126}& {M}_{138}\\ {M}_{7}& {M}_{19}& {M}_{31}& {M}_{43}& {M}_{55}& {M}_{67}& {M}_{79}& {M}_{91}& {M}_{103}& {M}_{115}& {M}_{127}& {M}_{139}\\ {M}_{8}& {M}_{20}& {M}_{32}& {M}_{44}& {M}_{56}& {M}_{68}& {M}_{80}& {M}_{92}& {M}_{104}& {M}_{116}& {M}_{128}& {M}_{140}\\ {M}_{9}& {M}_{21}& {M}_{33}& {M}_{45}& {M}_{57}& {M}_{69}& {M}_{81}& {M}_{93}& {M}_{105}& {M}_{117}& {M}_{129}& {M}_{141}\\ {M}_{10}& {M}_{22}& {M}_{34}& {M}_{46}& {M}_{58}& {M}_{70}& {M}_{82}& {M}_{94}& {M}_{106}& {M}_{118}& {M}_{130}& {M}_{142}\\ {M}_{11}& {M}_{23}& {M}_{35}& {M}_{47}& {M}_{59}& {M}_{71}& {M}_{83}& {M}_{95}& {M}_{107}& {M}_{119}& {M}_{131}& {M}_{143}\\ {M}_{12}& {M}_{24}& {M}_{36}& {M}_{48}& {M}_{60}& {M}_{72}& {M}_{84}& {M}_{96}& {M}_{108}& {M}_{120}& {M}_{132}& {M}_{144}\end{array}\right]}\)

or 36 values \({M}_{1}\), \({M}_{2}\),… \({M}_{36}\) in 2D_DIS_TR

\(M=\stackrel{\begin{array}{cccccc}{U}_{\mathit{x1}}& {U}_{\mathit{y1}}& {R}_{\mathit{z1}}& {U}_{\mathit{x2}}& {U}_{\mathit{y2}}& {R}_{\mathit{z2}}\end{array}}{\left[\begin{array}{cccccc}{M}_{1}& {M}_{7}& {M}_{13}& {M}_{19}& {M}_{25}& {M}_{31}\\ {M}_{2}& {M}_{8}& {M}_{14}& {M}_{20}& {M}_{26}& {M}_{32}\\ {M}_{3}& {M}_{9}& {M}_{15}& {M}_{21}& {M}_{27}& {M}_{33}\\ {M}_{4}& {M}_{10}& {M}_{16}& {M}_{22}& {M}_{28}& {M}_{34}\\ {M}_{5}& {M}_{11}& {M}_{17}& {M}_{23}& {M}_{29}& {M}_{35}\\ {M}_{6}& {M}_{12}& {M}_{18}& {M}_{24}& {M}_{30}& {M}_{36}\end{array}\right]}\)

Note:

The options M_T_L , M_TR_L, M_T_D_L, M_TR_D_L generally do not correspond to a modeling option with mechanical significance. They are available to import into Code_Aster of.*discretized mass matrices on a mesh* SEG2 determined by another software. In fact, point mass and inertia values (mesh POI1 ) are usually assigned by M_T_D_N or M_TR_D_N.

12.3.5. Operand AMOR_HYST#

◊ AMOR_HYST = amorh

Allows you to assign a coefficient to a discrete element to build a complex stiffness matrix (modeling of hysteretic damping) the constructed matrix is:

\((1+{\mathrm{j.amor}}_{h})\mathrm{.}K\)

where \(K\) is the K_* matrix whose values are provided in the same occurrence of the DISCRET keyword. The complex stiffness matrix will actually be built during a call to CALC_MATR_ELEM [U4.61.01] with the AMOR_HYST option (see test SDLD313) and [R5.05.04].

12.3.6. Operand REPERE#

◊ REPERE =/”LOCAL”,

/”GLOBAL”,

By default the values of the matrices provided for the discrete elements are used to express the corresponding quantities in the REPERE =” GLOBAL “.

If we want to define a particular coordinate system in a node (or POI1 mesh) we will specify REPERE =” LOCAL “by defining this coordinate system with the keyword ORIENTATION [§ 10].

For a matrix defined on a SEG2 cell, the operand REPERE =” LOCAL “makes it possible to refer to the local coordinate system attached to the mesh (initial node, final node) supplemented, if necessary, by a spin angle defined by the keyword ORIENTATION [§ 10].