5. Implementation of a calculation CZM#
The cohesive models presented here have been the subject of a number of calculations in various mechanical problems, most often on target structures (test specimens). Here are a few examples:
Initiation and propagation of cracks in an elastic or elastoplastic beam in fragile rupture,
propagation of a crack under cyclic loading in an elastoplastic beam to model fatigue as well as the overload effect.
Propagation of a plane 3D crack in brittle fracture or fatigue, followed by the crack front.
Modeling the dynamic propagation of cracks in a bimaterial.
Cracking and sudden propagation of two cracks through a perforated plate (quasi-static calculations with control).
Tearing off a rigid frame.
In this part, we present the various tests based on the cohesive elements in Code_Aster and then we comment on one of them.
5.1. List of test cases with cohesive models#
TEST ELEMENTAIRE, A ELEMENT COHESIF, AND A ELEMENT ELASTIQUE
ssnap118a: EJ 2D PLAN, LOI CZM_EXP_REG
ssnp118b: EJ 3D (HEXA), LOI CZM_EXP_REG
ssnap118c: EJ 3D (PENTA), LOI CZM_EXP_REG
ssnap118d: EJ 2D PLAN, LOI CZM_LIN_REG
ssnp118e: EJ 3D (HEXA), LOI CZM_LIN_REG
ssnp118f: EJ 3D (PENTA), LOI CZM_LIN_REG
ssnp118g: EI 2D PLAN, LOIS CZM_OUV_MIX AND CZM_TAC_MIX
ssnp118h: EI 3D (HEXA), LOIS CZM_OUV_MIX AND CZM_TAC_MIX
ssnp118i: EI 3D (PENTA), LOIS CZM_OUV_MIX AND CZM_TAC_MIX
ssnp118j: EI 2D PLAN, LOI CZM_FAT_MIX
ssnp118k: EI 3D (HEXA), LOI CZM_FAT_MIX
ssnp118l: EI 3D (PENTA), LOI CZM_FAT_MIX
ssnp118m: EI 2D PLAN, LOI CZM_TRA_MIX
ssnp118n: EI 3D (HEXA), LOI CZM_TRA_MIX
ssnp118o: EI 3D (PENTA), LOI CZM_TRA_MIX
ssnp118q: EI 2D PLAN, LOI CZM_EXP_MIX
ssnp118r: EI 3D (HEXA), LOI CZM_EXP_MIX
ssnp118s: EI 3D (PENTA), LOI CZM_EXP_MIX
MISE IN OEUVRE OF THE LOI OF INTERFACE ELASTIQUE SUR A CUBE
sslv01a: EI3D (PENTA), LOI CZM_ELAS_MIX
sslv01b: 2D UI (TRIA), LOI CZM_ELAS_MIX
ARRACHEMENT of UNE ARMATURE RIGIDE
ssna115a: ED 2D AXIS, LOI CZM_EXP
ssna115b: EJ 2D AXIS, LOI CZM_LIN_REG
ssna115c: EI 2D AXIS, LOI CZM_TAC_MIX
EPROUVETTE AXISYMETRIQUE ENTAILLEE (AE) ELASTOPLASTIQUE
ssna120a: EI 2D AXIS, LOI CZM_TRA_MIX
FISSURATION OF UNE PLAQUE, COMPARAISON AVEC SOLUTION ANALYTIQUE
ssnp128a: ED 2D PLAN, LOI CZM_EXP
FISSURATION BRUTALE FROM UNE PLAQUE TROUEE AVEC PILOTAGE FROM CHARGEMENT
ssnop133a: EJ 2D PLAN, LOI CZM_EXP_REG
ssnp133b: ED 2D PLAN, LOI CZM_EXP
ssnp133c: EI 2D PLAN, LOI CZM_OUV_MIX
POUTRE Compact Tension (CT) 2D ELASTOPLASTIQUE
ssnp151a: EI 2D PLAN, LOI CZM_TRA_MIX
POUTRE Compact Tension (CT) 3D ELASTOPLASTIQUE
ssnp151b: EI 3D (HEXA), LOI CZM_TRA_MIX
POUTRE Double Cantilever Beam (DCB) 2D ELASTOPLASTIQUE, MONOTONE AND FATIGUE
ssnp139a: EI 2D PLAN, LOI CZM_OUV_MIX
ssnp139b: EI 2D PLAN, LOI CZM_FAT_MIX (example commented below)
POUTRE Double Cantilever Beam (DCB) 3D ELASTIQUE
ssnv199a: EJ 3D (HEXA), LOI CZM_EXP_REG
ssnv199b: EJ 3D (PENTA), LOI CZM_EXP_REG
ssnv199c: EJ 3D (HEXA), LOI CZM_LIN_REG
ssnv199d: EJ 3D (PENTA), LOI CZM_LIN_REG
ssnv199e: EI 3D (HEXA), LOI CZM_OUV_MIX
ssnv199f: EI 3D (PENTA), LOI CZM_OUV_MIX
PROPAGATION 2D DYNAMIQUE AND DEPENDANCE IN TEMPERATURE OF THE LOI COHESIVE
sdns105a.com: EJ 2D PLAN, LOI CZM_EXP_REG
POUTRE ENTAILLEE IN FLEXION 3 POINTS
ssnp166a.com: EI 2D PLAN, LOI CZM_EXP_MIX
5.2. Commented example, beam DCB in fatigue#
Here we present test SSNP139, modeling b, corresponding to the simulation of crack propagation by fatigue in a two-dimensional Double Cantilever Beam (DCB). The diagram of the mechanical problem is presented in FIG. 5.2 and then the command file commented with reference to the various tips given above. The passages specifically dedicated to cohesive elements are highlighted in red.
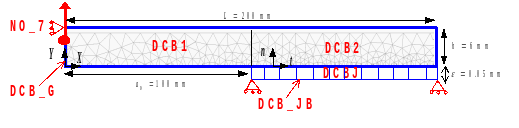
Figure 5.2: DCB geometry and boundary conditions.
##################################################################################################***
# POUTRE DCB 2D PLASTIQUE AVEC ELEMENTS FROM INTERFACE TO FATIGUE: LOI CZM_FAT_MIX
##################################################################################################***
DEBUT (CODE =_F (NOM = “SSNP139B”))
# LOIS OF COMPORTEMENT OF THE DCB AND OF THE FISSURE COHESIVE (see 6 )
loi_vol=” VMIS_ISOT_LINE “
loi_czm=” CZM_FAT_MIX “
# NOMBRE FROM CYCLES MAXIMUM
nb_cy_max= 101
**# INSTANT FINAL (IMPAIRE AND INFERIEUR A 2*nb_cy_max-1) **
end=5
# NOMBRES FROM PAS (see 21 )
bpas = 5*fine
# ON ARCHIVE LES SOMMETS (see 21 )
nbarch = (fin-1) /2
# VALEURS OF THE FONCTION OF CHARGEMENT
Delta_u = 0.4
val_inf = 0.0
val_sup = val_inf + delta_U
val_surch = 1.2
# NUM FROM CYCLE POUR CHANGEMENT AMPLITUDE VARIABLE
# to do a single overload at the moment 2*x+1 put: nb_cy_1 = x, nb_cy_2 = x+1, nb_cy_3= … ,
# below, overload at time 23.
nb_cy_1 = 11
nb_cy_2 = 12
nb_cy_3 = nb_cy_max
# PARAMETRES MECANIQUES FROM THE LOI CZM (test values, see 15 )
tenac = 0.259/2# we only model a half crack (division by two of the material Gc see 15)
sigc = 35
dc = 2*tenac/sigc
# PARAMETRES NUMERIQUES DES ELEMENTS D’INTERFACE (see 15 )
ri_gli=10
pen_lag=100
# PARAMETRES FROM LOI ELASTOPLASTIQUE (test values)
young = 200000
weight = 0.3
Play = 30
nut = 3577
PRE_GMSH ()
MA0 = LIRE_MAILLAGE ()
# PASSAGE FROM MAILLAGE TO QUADRATIQUE (see 9 )
MA = CREA_MAILLAGE (MAILLAGE = MA0, LINE_QUAD ** = _F (TOUT =” OUI “))
# DEFINITION DES GROUPES
MA = DEFI_GROUP (
reuse = MA,
MAILLAGE = MY,
CREA_GROUP_MA = (
# LINES
_F (NOM = “DCB_G”, GROUP_MA = “GM981”), # LIEU FROM CHARGEMENT IMPOSE
_F (NOM = “DCB_JB”, GROUP_MA = “GM984”), # FACES POUR CONDITION FROM SYMETRIE
# SURFACES
_F (NOM = “DCB1”, GROUP_MA = “GM988”), # PARTIE VOLUMIQUE GAUCHE FROM THE POUTRE
_F (NOM = “DCB2”, GROUP_MA = “GM989”), # PARTIE VOLUMIQUE DROITE FROM THE POUTRE
_F (NOM = “DCBJ”, GROUP_MA = “GM990”), # ELEMENTS FROM INTERFACE
),
CREA_GROUP_NO = (
_F (NOM = “DCB_G”, GROUP_MA = “GM981”),
_F (NOM = “NO_7”, GROUP_MA = “GM954”), # NOEUD BLOQUE DANS LA DIRECTION X
)
)
# ORIENTATION DES ELEMENTS D’INTERFACE (VOIR 10 )
MA= MODI_MAILLAGE (reuse =MA,
MAILLAGE =MY,
ORIE_FISSURE =_ F (GROUP_MA = “ DCBJ “),
)
# AFFECTATION DES MODELISATIONS
MO= AFFE_MODELE (
MAILLAGE =MY,
AFFE = (
_F (
GROUP_MA = (“DCB1”, “DCB2”, “DCB_G”),
PHENOMENE = “MECANIQUE”,
MODELISATION = “D_ PLAN “
),
_F (
GROUP_MA = “DCBJ **”,
PHENOMENE = “MECANIQUE”,
MODELISATION = “PLAN_INTERFACE “# MODELISATION PLAN POUR LES ELEMENTS d’INTERFACE
),
))
# DEFINITION FROM THE POSITION FROM THE FISSURE DANS THE REPERE GLOBAL (see 7 )
ORIEN_FI = AFFE_CARA_ELEM (MODELE =MO,
MASSIF =( _F (GROUP_MA =” DCBJ “,
ANGL_REP =( 90, 0.0)))))); # IN 2D UNIQUEMENT THE PREMIER ANGLE
# DEFINITION AND AFFECTATION FROM MATERIAU
# ICI A SEUL MATERIAU, ON PEUT AUSSI CREER DEUX MATERIAUX DIFFERENTS ONE POUR THE, ON VOLUME AND THE** AUTRE
# POUR THE FISSURE COHESIVE
MATE = DEFI_MATERIAU (
ELAS =_F (
E = young,
NU = weight),
ECRO_LINE =_F (
D_ SIGM_EPSI =nut,
SY=sPlas),
RUPT_FRAG = _F ( # MOT CLE POUR LES CZM IN RUPTURE FRAGILE
GC = tenac, # PARAMETRE MATERIAU (see 15)
SIGM_C = sigc, ** # PARAMETRE MATERIAU (see 15)
PENA_LAGR = pen_lag, # PARAMETRE NUMERIQUE (see 15)
RIGI_GLIS = ri_gli, # PARAMETRE NUMERIQUE (see 15)
))
CM= AFFE_MATERIAU (
MAILLAGE =MY,
AFFE =_F (
GROUP_MA = (“DCB1”, “DCB2”, “DCBJ”),
MATER = MATE),
)
# CHARGEMENTS
SYMETRIE = AFFE_CHAR_MECA (
MODELE = MO,
FACE_IMPO = (_F (GROUP_MA =” DCB_JB “, DY = 0)) # CONDITION FROM SYMETRIE SUR THE LEVRE INFERIEURE
)
TRACTION = AFFE_CHAR_MECA (
MODELE = MO,
DDL_IMPO = (_F (GROUP_NO = “NO_7”, DX = 0)), # BLOCAGE FROM MODE RIGIDE
FACE_IMPO = (_F (GROUP_MA = “DCB_G”, DY = 1), # DIRECTION FROM CHARGEMENT
))
# DEFINITION OF THE LISTE OF INSTANT
deb=- (val_INF/delta_u) —0.0000001 # VALEUR DU DEBUT DES INSTANTS PERMETTANT FROM ATTEINDRE UN NIVEAU
# FROM CHARGEMENT val_inf to INSTANT 0 PROGRESSIVEMENT
L_ INST = DEFI_LIST_REEL (DEBUT = deb,
INTERVALLE =(
_F (JUSQU_A = 0, NOMBRE = 10),
_F (JUSQU_A = end, NOMBRE = bpas),
))
ARCHIVAGE FROM INSTANT 0 AND DES INSTANTS IMPAIRES (SOMMETS FROM CHAQUE CYCLE)
INS_ARCH = DEFI_LIST_REEL (DEBUT = deb,
INTERVALLE =(
_F (JUSQU_A = 0, NOMBRE = 1),
_F (JUSQU_A = 1, NOMBRE = 1),
_F (JUSQU_A = end, NOMBRE = nbarch),
))
# DEFINITION FROM EVOLUTION CYCLIQUE FROM CHARGEMENT
# a: FONCTION AMPLITUDE CONSTANTE AVEC SURCHARGE (see 21 )
a = []
for i in xrange (nb_cy_1) :
a.extend ((2*i, val_inf,2*i+1, val_sup))
for i in range (nb_cy_1, nb_cy_2) :
a.extend ((2*i, val_inf,2*i+1, val_surch))
for i in range (nb_cy_2, nb_cy_3) :
a.extend ((2*i, val_inf,2*i+1, val_sup))
FCT_FAT ** = DEFI_FONCTION (
NOM_PARA = “INST”,
PROL_GAUCHE =” LINEAIRE “,
VALE = a,
)
DEFLIST = DEFI_LIST_INST (DEFI_LIST =_F (LIST_INST =L_ INST),
ECHEC =_F (
SUBD_METHODE =” UNIFORME “,
SUBD_PAS = 3,
SUBD_PAS_MINI = 1.E-10,
SUBD_NIVEAU =10,
),)
# CALCUL NON LINEAIRE
U= STAT_NON_LINE (
MODELE = MO,
CHAM_MATER = CM,
CARA_ELEM = ORIEN_FI, **#**# AFFECTATION DES CARACTERISTIQUES FROM ORIENTATION AUX ELEMENTS D’INTERFACE **
EXCIT = (
_F (CHARGE = SYMETRIE),
_F (CHARGE = TRACTION, FONC_MULT = FCT_FAT),
),
COMPORTEMENT = (
_F (RELATION = law_vol, GROUP_MA = (“DCB1”, “DCB2”)),
_F (RELATION = loi_czm, GROUP_MA = “DCBJ **”),
),
INCREMENT = _F (LIST_INST = DEFLIST,
INST_FIN = end,
),
NEWTON = _F (MATRICE = “TANGENTE”, REAC_ITER =1),
CONVERGENCE = _F (
RESI_REFE_RELA = 1.E-6,
SIGM_REFE = sigc, ** # CONTRAINTE FROM REFERENCE (see 16)
DEPL_REFE = dc, # DEPLACEMENT DE REFERENCE (see 16)
ITER_GLOB_MAXI = 8,
),
SOLVEUR = _F (
METHODE = “MUMPS”, PCENT_PIVOT = 100), # SOLVEUR MUMPS NECESSAIRE POUR LES EI (see 17 )
ARCHIVAGE = _F (LIST_INST = INS_ARCH
))
# POST_TRAITEMENT: IMPRESSIONS FROM INDICATEUR D’ENDOMMAGEMENT V3 AND FROM POURCENTAGE FROM ENERGIE DISSIPEE V4 (see 22 )
IMPR_RESU (FORMAT =” RESULTAT “, RESU =( _F (RESULTAT =U,
NOM_CHAM =” VARI_ELGA “,
INST =end,
NOM_CMP =( “V3”, “V4”))))
FIN (FORMAT_HDF =” OUI “)