3. Laws of contact and friction#
In this chapter, we will write the various forms equivalent to the standard touch-friction laws (Signorin’s law and Coulomb’s law). The demonstration of equivalence between the various forms (Signorin, Coulomb, augmented Lagrangian, stabilized Lagrangian) is available in [].
In Code_Aster, the « stabilized Lagrangian » forms are used.
3.1. Contact law#
3.1.1. Signorin’s law#
The*Signorini law* for unilateral contact is written as:
: label: eq-108
left{{P} ^ {C}right}right}mathrm {equiv}mathrm {equiv}mathrm {{}begin {array} {cc} {lambda} _ {n}the 0& (b)\ {lambda} _ {n} {d} _ {n}mathrm =} 0& (c)end {array}
where \({d}_{n}\) is the algebraic game defined by equation () and \({\lambda }_{n}\) is the contact pressure. The graph of Signorin’s law is shown on the. The first condition transcribes the condition of non-adherence and the second condition reflects impenetrability.
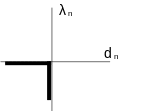
|
Figure 4 : Graph of the law of unilateral contact of Signorini |
The contact problem thus posed introduces a non-univocal relationship (\({\lambda }_{n}\) is not a step in \({d}_{n}\)), semi-definite positive and non-differentiable in \({\lambda }_{n}\mathrm{=}{d}_{n}\mathrm{=}0\). Signorin’s law of contact is equivalent to a law of behavior. It is analogous to the case of perfect rigid plasticity. It should therefore be noted that game \({d}_{n}\) is equivalent to measuring a deformation and that it must therefore be objective.
3.1.2. Contact law — Convex analysis#
Using the tools of convex analysis, we can write Signorin’s law in the following form:
: label: eq-109
left{{P} _ {mathit {cvxe}}} ^ {C}right}mathrm {equiv}mathrm {{}begin {array} {cc} {lambda} {lambda} _ {lambda} _ {n}lambda} _ {n}mathrm {lambda}} _ {n}mathrm {text {-}}} ({d} _ {n}) & (a)\ {d}} _ {n}mathrm {in}mathrm {partial} {I} _ {{mathrm {390}}}} ^ {text {-}}} ^ {text {-}}} ^ {text {-}}}} ^ {text {-}}}} ({text {-}}}}} ({lambda} _ {n}) & (b)end {array}} _ {{mathrm {390}}}} ^ {text {-}}} ^ {text {-}}} ^ {text {-}}}}
\(\mathrm{\partial }\) designating the subdifferential and \({I}_{K}\) the indicative function of the convex \(K\):
: label: eq-110
{I} _ {K} (x)mathrm {=}mathrm {=}mathrm {in}mathrm {{}}begin {array} {x}end {array} xmathrm {in} xmathrm {in} K\begin {in} K\begin {array} {in} K\ begin {array} {cc}begin {array} {cc}mathrm {infty} &text {si}end {array}} xend {array} xmathrm {notin} Kend {array}
The Signorin contact law consists of inequalities (search for a solution in a given convex), this writing is used when solving the contact problem by optimization methods under constraints: it is the preferred methodology for discrete formulations in Code_Aster. In the continuous method, a form of semi-regularization is used using projection operators in a given convex.
3.1.3. Law of contact — Projection#
The augmented Lagrangian method applied to contact consists in using the projection onto convex \({\mathrm{ℝ}}^{\text{-}}\) of a quantity called increased contact multiplier \({g}_{n}\), defined by:
: label: eq-111
{g} _ {n}mathrm {=} {lambda} _ {lambda} _ {n}mathrm {-} {rho} _ {n} _ {d} _ {n}
where \({\rho }_{n}\) is a strictly positive real, homogeneous to a force on a unit of volume:
: label: eq-112
left [{rho} _ {n}right]mathrm {=}frac {mathrm {[} Fmathrm {]}}} {{mathrm {[}} Lmathrm {[}} Lmathrm {]}}} ^ {3}}
The Signorin \({P}^{C}\) problem is then rewritten:
The idea of this formulation is to replace the non-differentiable energetic part of the contact, by the square of the projection of \({g}_{n}\) in an appropriate convex, which makes the functional energy of the augmented Lagrangian differentiable. The projection operator explicitly applies to:
: label: eq-114
{mathit {Proj}} _ {{mathrm {492}}} ^ {text {-}}} ({g} _ {n})mathrm {=}mathrm {{}begin {array}begin {array} {c}}} {c} {g}} _ {n}mathrm {le}{}{}begin {array} {c} {c} {g}} {g} _ {n}mathrm {le} 0\ 0text {if} {g} _ {n} >0end {array}
The increased contact multiplier \({g}_{n}\) is a line in \(({d}_{n},{\lambda }_{n})\) space. With the projection operator \({\mathit{Proj}}_{{\mathrm{ℝ}}^{\text{-}}}(x)\), we are back to the Signorin graph. \({\mathit{Proj}}_{{\mathrm{ℝ}}^{\text{-}}}(x)\) is continuous on \({\mathrm{ℝ}}^{\text{-}}\) and almost everywhere differentiable.
3.1.4. Law of contact — stabilized Lagrangian#
The idea of the formulation by sign field (also called stabilized formulation) is to dissociate the status of a contact point from the value of the augmented Lagrangian. The same multiplier \({g}_{n}\) is introduced as in the case of the augmented Lagrangian (equation). The sign field (« level-set ») noted \({S}_{u}^{x}\) is defined by the following expression:
: label: eq-115
{S} _ {u} ^ {{g} _ {n}}mathrm {=}mathrm {=}mathrm {{}begin {array} {cc} 1&text {si} {c} 1&text {si} {g} {g} _ {g} _ {g} _ {n} _ {n} _ {n}mathrm {le} 0end {array} {cc} {c}begin {array} {cc} 1&text {si} {g} 0&text {si} {g} _ {g} _ {g} _ {n} _ {n}}mathrm {le} 0end {array} {cc} {c}begin {array} {cc} 1&text {si} {} _ {n} >0end {array}end {array}
This operator is the characteristic function of the variable \({g}_{n}\) on the convex \({\mathrm{ℝ}}^{\text{-}}\). It is not differentiable. The Signorin \({P}^{C}\) problem is then rewritten:
: label: eq-116
left{{P} _ {mathit {stab}}} ^ {C}right}mathrm {equiv}mathrm {{}begin {array} {cc} {lambda} {lambda} _ {lambda} _ {lambda} {lambda} {lambda} {lambda} {lambda} {lambda} {lambda} {lambda} {lambda}} {lambda} _ {lambda}} {lambda} _ {lambda}} _ {lambda} _ {lambda}} _ {lambda} _ {lambda}} {lambda} _ {lambda}} {lambda} _ {lambda}} {lambda} _ {lambda} {-} {rho} _ {n} {lambda} _ {d} _ {n})mathrm {=} 0& (a)\ {g} _ {n}mathrm {=} {lambda} _ {lambda} _ {lambda} _ {n}} _ {u} _ {u} _ {u} _ {u})mathrm {-} {n} 0& (a)\ {g} _ {n} _ {u} ^ {{g} _ {n}}mathrm {=}mathrm {=}mathrm {{}begin {array} {c}begin {array} {cc} 1&text {si} {g} _ {g} _ {g} _ {n} _ {n} _ {n} 0mathrm {le} 0mathrm {le} 0end {le} 0end {array} {c} {c}begin {array} {cc} 1&text {si} {g}} _ {n} _ {n} >0end {array}end {array} & (c)end {array}
The \({g}_{n}\) increased contact multiplier is a line. The irregular nature of the law of contact is the non-differentiable character coming from the sign field. \({S}_{u}^{x}\) is almost everywhere continuous (except in \(x\mathrm{=}0\)) and almost everywhere differentiable. The two operators \({S}_{u}^{x}\) and \({\mathit{Proj}}_{{\mathrm{ℝ}}^{\text{-}}}(x)\) are linked by a simple relationship:
: label: eq-117
x {S} _ {u} ^ {x}mathrm {=} {mathit {Proj}} _ {{mathrm {zzy}}} ^ {text {-}}} ^ {text {-}}}} (x)
It is this form that is used in*Code_Aster*.
3.2. Law of friction#
3.2.1. Coulomb’s law#
To represent the phenomena of friction, we use the Coulomb law which is written as follows:
where \(\mu\) is called Coulomb coefficient of friction*(assumed to be constant and isotropic), and \({v}_{\tau }\) is the*tangent relative velocity*, defined as the projection in the tangential plane to the surface at the point of contact of the jump in speed of solid \(1\) with respect to solid \(2\). When the contact is slippery, as \({\lambda }_{n}\) is always hypothetically negative, you can write:
The quantity \(\frac{{v}_{\tau }}{\mathrm{\parallel }{v}_{\tau }\mathrm{\parallel }}\) corresponds to the direction of sliding, which is unknown, but which we know takes place in the tangential plane made up of the two vectors \(({t}_{1},{t}_{2})\). The third law, analogous to that of equation (c) introduced for contact, imposes the nullity of the frictional forces when there is no contact. The graph of Coulomb’s law of friction is shown on the.
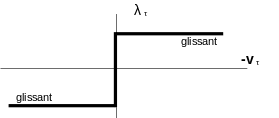
|
Figure 5 : Graph of the Coulomb law of friction** |
Friction induces the concept of threshold. The relationship introduced by Coulomb friction is*non-univocal* and non-differentiable. The expression for \({v}_{\tau }\) is given by:
The tangential speed jump \({v}_{\tau }\) is not objective (see []) . Strictly speaking, \({v}_{\mathrm{gliss}}\) should be used (see p. 13). However, these two definitions are the same when there is contact (\({d}_{n}=0\)). Coulomb’s law of friction is written in speed and not in movement, unlike Signorin’s law. This constitutes one of the difficulties to be considered in the case of a quasi-static resolution of the touch-friction problem. It is not possible to directly replace speed by displacement without assuming that the loading in the contact zone varies monotonically, which, in practice, is an assumption that is impossible to satisfy for any loading of the structure.
However, we can write Signorin’s law in incremental form, considering the displacement increment, this way of doing things is correct in terms of respecting Coulomb’s law. But the difficulty is that by not knowing a priori the value of the total quantity of contact pressure, the Coulomb problem must be solved in two stages.
3.2.2. Law of friction — Convex analysis#
Using the tools of convex analysis, we can write Coulomb’s law in the following form:
: label: eq-121
left{{P} _ {mathit {cvxe}}} ^ {F}right}mathrm {equiv}mathrm {{}begin {array} {cc} {lambda} {lambda} _ {lambda} _ {lambda}} _ {cc} {lambda} {lambda}} {lambda} _ {lambda}} _ {lambda} _ {lambda} _ {lambda}} _ {lambda} _ {lambda} _ {lambda} _ {n})} _ ({v} _ {tau}) & (a)\ {v} _ {v} _ {tau} _ {tau}mathrm {partial} {I} _ {{C} ^ {text {*}} {text {*}}} ({text {*}}}} ({lambda} _ {tau})} ({lambda} _ {tau}) & (b)end {*}}} ({lambda} _ {tau}) & (b)end {*}}} ({lambda} _ {tau}) & (b)end {*}}} ({lambda} _ {tau}) & (b)end {*}}
With the convex \(C({\lambda }_{n})\) representing the Coulomb cone:
: label: eq-122
C ({lambda} _ {n})mathrm {=}left{mathrm {forall} {lambda} _ {tau}text {such as}mathrm {parallel} {parallel} {parallel} {parallel}}mathrm {tau}mathrm {mid}right}
3.2.3. Law of friction — Projection#
The augmented Lagrangian method applied to friction is similar to the case of contact, except that the convex in question changes. Consider the increased friction multiplier \({g}_{\tau }\), defined by:
where \({\rho }_{\tau }\) is a strictly positive real, homogeneous to a force on a unit of volume:
The Coulomb problem \({P}^{F}\) is then rewritten:
: label: eq-125
left{{P} _ {{mathit {Proj}}} _ {C ({lambda}} _ {n})}} ^ {F}right}mathrm {equiv}mathrm {{}mathrm {{}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {equiv}mathrm {C ({lambda} _ {n})} ({g} _ {tau})} & (a)\ {g} _ {tau}mathrm {=} {lambda} _ {tau} _ {tau} _ {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau} + {tau}
The projection operator is not orthogonal:
3.2.4. Law of friction — Normalized projection#
In the contact, we used the same definition of the increased multiplier between the augmented Lagrangian formulation and the stabilized Lagrangian formulation. On the other hand, for the friction, we will proceed differently. First, we introduce a quantity \(\Lambda\) called Lagrange semi-multipliator:
: label: eq-127
{lambda} _ {tau}mathrm {=}mu {lambda} _ {n}Lambda
This standardized quantity belongs to the unit ball:
It is called semi -Lagrange multiplier because this quantity has two meanings:
In the case of adherent friction, \(\Lambda\) represents the adhesive force density. It is therefore formally the Lagrange multiplier associated with the adhesion condition (zero tangential relative speed);
In the case of sliding, \(\Lambda\) indicates the direction of sliding (normalized) and we have \(\Lambda \mathrm{=}\frac{\mathrm{-}{\lambda }_{\tau }}{\mathrm{\parallel }{\lambda }_{\tau }\mathrm{\parallel }}\mathrm{=}\frac{{v}_{\tau }}{\mathrm{\parallel }{v}_{\tau }\mathrm{\parallel }}\); which is not the definition of a Lagrange multiplier in the « classical » sense (see p. 3.2.3);
Note that \({\lambda }_{n}\) is always negative or zero (usual pressure convention), \({\lambda }_{\tau }\) has the opposite sign to \(\Lambda\), which indicates the direction of sliding. This change in variable makes it possible to go from the unknown to an effort tangent to the direction of this effort. Therefore, we introduce the semi-multiplier increased by friction \({h}_{\tau }\) (to distinguish it from the « classical » \({g}_{\tau }\), see () such that:
: label: eq-129
{h} _ {tau}mathrm {=}Lambda + {rho} _ {t} {v} _ {tau} _ {tau}
It should be noted that the increase coefficient \({\rho }_{t}\) has a different unit than \({\rho }_{\tau }\) in the case of increased Lagrangian. Indeed, it is written as the ratio of a time over a length:
: label: eq-130
left [{rho} _ {t}right]mathrm {=}frac {mathrm {[} Tmathrm {]}}} {mathrm {[}} Lmathrm {[}} Lmathrm {]}}
In the augmented Lagrangian formulation, the increase coefficient \({\rho }_{\tau }\) is in the same unit as the contact increase coefficient (see). The Coulomb problem \({P}^{F}\) is rewritten:
: label: eq-131
left{{P} _ {{mathit {Proj}}} _ {B (mathrm {0,} 1)}}} ^ {F}right}mathrm {equiv}mathrm {{}mathrm {}mathrm {}mathrm {}mathrm {equiv}mathrm {}mathrm {equiv}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {}mathrm {} 0,} 1)} ({h} _ {tau}) & (a)\ {h}) & (a)\ {h} _ {tau}mathrm {=}Lambda + {rho} _ {tau} _ {tau}) & (b)end {array} _ {tau}
This projection operator is orthogonal:
: label: eq-132
{mathit {Proj}} _ {B (mathrm {0,} 1)} ({h} _ {tau})mathrm {=}mathrm {{}begin {array} {array} {c} {array} {c} {h} _ {tau} _ {tau}mathrm {in} B (mathrm {0,} 1)\ taumathrm {=}frac {{h}} _ {tau}} {mathrm {parallel} {h} _ {tau}mathrm {parallel}}mathrm {parallel}}}text {parallel}}}text {parallel}}}text {parallel}}}text {parallel}}}text {parallel}}}text {si} {h} _ {tau} _ {tau}} B (mathrm {0,} 1)mathrm {parallel}}}mathrm {parallel}}}mathrm {parallel}}}mathrm {parallel}}}mathrm {parallel}}}
Note:
: label: eq-133
taumathrm {=}frac {{h} _ {tau}} {mathrm {parallel} {h} _ {tau}frac {{h}}frac {{h}} _ {tau}mathrm {parallel}}
We will proceed to calculate the variation with respect to variable \(x\):
We will note the projection matrix on the unit ball:
3.2.5. Law of friction — stabilized Lagrangian#
The sign field (« level-set ») noted \({S}_{f}^{{h}_{\tau }}\) is defined by the following expression:
This operator is the characteristic function of the variable \({h}_{\tau }\) on the convex \(B(\mathrm{0,}1)\). It is not differentiable. The Coulomb problem \({P}^{F}\) is then rewritten:
The stabilized Lagrangian form is a exact formulation of the friction problem. It is this form that is used in*Code_Aster*.
3.3. Contact-friction law#
3.3.1. Augmented Lagrangian#
We write the augmented Lagrangian for the touch-friction problem. Consider convex \(K\) such that:
: label: eq-138
Kmathrm {=}left{lambda;lambdamathrm {=} {lambda} _ {tau} + {lambda} _ {n} ntext {with} {lambda} {with} {lambda} _ {lambda} _ {lambda} _ {lambda} _ {lambda} _ {lambda}}text {with} {lambda} _ {lambda} _ {lambda} _ {lambda}}text {with} {lambda} _ {lambda} _ {lambda}}text {with} {lambda} _ {lambda}}text {with} {lambda} _ {lambda}} {with} {lambda}}} _ {tau}mathrm {in} C ({lambda} _ {n})right}
So the augmented Lagrangian for the touch/friction problem is written:
The projection on convex \(K\) explicitly applies to:
Case (a) corresponds to the adherent contact, case (b) is the sliding contact and case (c) is the case without contact (or friction).
3.3.2. Stabilized Lagrangian#
We write the stabilized Lagrangian for the touch/friction problem:
: label: eq-141
left{{P} _ {mathit {stab}}} ^ {mathit {stab}} ^ {mathit {CF}}rightmathrm {equiv}mathrm {{}begin {array} {{array} {cc} {cc}} {cc} {lambda}} {cc} {lambda}} _ {n}} {cc} {lambda} _ {n}} _ {n}} ({lambda}} _ {n}} {n}mathrm {-} {rho} _ {n} {rho} _ {d} _ {n})mathrm {=} 0& (a)\ (1mathrm {-} {S}} {S}} _ {n}} _ {n}} _ {n}} _ {n}} _ {n}} _ {n} _ {n}} _ {n}} _ {n}} _ {n}}left{(1)mathrm {-} {S} _ {f} ^ {{h} ^ {{h} _ {tau}})Lambdamathrm {-} {rho} _ {t} {v} _ {tau} {S} {S} {S} {S} {S} {S} {S} {S} {S} {S} _ {f} ^ {f} ^ {f} ^ {f} ^ {{h} _ {tau}})tauright})tauright}}mathrm {=} 0& (b)\ {g} _ {n} {lambda} _ {n}mathrm {-}mathrm {-} {-} {rho}} _ {rho} _ {tau} {rho} _ {rho} _ {tau}mathrm {=}Lambda + {rho} _ {t} {v} _ {tau} & (d)\ {lambda} _ {lambda} _ {tau}mathrm {=}mu {lambda} _ {n}Lambda & (e)\taumathrm {=}frac {{h} _ {tau}}} {mathrm {parallel}}} {tau}} {tau}mathrm {parallel}} & (f)end {array}} {tau}} {tau}} & (f)end {array}} {tau}}
With both sign fields:
: label: eq-142
{S} _ {u} ^ {{g} _ {n}}mathrm {=}mathrm {=}mathrm {{}begin {array} {cc} 1&text {si} {c} 1&text {si} {g} {g} _ {g} _ {g} _ {n} _ {n} _ {n}mathrm {le} 0end {array} {cc} {c}begin {array} {cc} 1&text {si} {g} 0&text {si} {g} _ {g} _ {g} _ {n} _ {n}}mathrm {le} 0end {array} {cc} {c}begin {array} {cc} 1&text {si} {} _ {n} >0end {array}end {array}
It is this form that is used in*Code_Aster*.
3.3.3. Differences between increased Lagrangian and stabilized Lagrangian#
Both scripts belong to the category of unconstrained optimization methods. The main differences come from the use of a « sign field » (or level-set), and, for friction, from a change in variable reducing the Coulomb disk to a disk with a unit radius.
By dissociating the writing of augmented Lagrangian from that of status (contact/detachment and adherent/sliding), this allows us to introduce the unknowns of statuses*explicitly in the case of stabilized Lagrangian;
In stabilized Lagrangian, a friction semi-multiplier is used, which has the main effect of having a different unit between Lagrangian increased by friction :math:`{rho }_{t}` and Lagrangian increased by contact :math:`{rho }_{n}`; it is this form that is used in*Code_Aster.
We will find the demonstration of the equivalence between these two scriptures in [].