2. Cinematics

2.1. Solid state kinematics

Two \({B}^{i}(i=\mathrm{1,2})\) solids are considered to be deformable in contact with friction. In their initial configuration, these two solids occupy the adhesion of two domains \({O}_{0}^{1}\) and \({\Omega }_{0}^{2}\) of \({\mathrm{ℝ}}^{3}\) and, in their current configuration at time \(t\), the adhesion of \({O}_{t}^{1}\) and \({O}_{t}^{2}\) (also included in \({\mathrm{ℝ}}^{3}\)), respectively. It is assumed that, in their initial configuration, these two solids are in a natural state, i.e. without residual stresses or pre-deformations. Consider a material particle \({M}^{i}\) from solid \({B}^{i}\), identified by the vector \({p}^{i}\) in the initial configuration. \({\varphi }_{t}^{i}\) refers to the transformation at time \(t\) of the solid \({B}^{i}\), this application transports the particle \({M}^{i}\) to position \({x}_{t}^{i}\) in the current configuration. We have:

(2.1)\[\begin{split} \ begin {array} {cc} {\ varphi} _ {t}} _ {t} ^ {i} _ {i} _ {0} ^ {i} _ {0} ^ {i}\ mathrm {\ times}\ left [\ mathrm {\ times}\ left [\ mathrm {0,} t\ right]\ to {\ Omega} _ {t} ^ {i}\ mathrm {i}\ mathrm {times}\ left [\ mathrm {times}\ left [\ mathrm {0,} t\ right]\ to {\ Omega} _ {t} ^ {i}\ mathrm {i}\ mathrm {times}\ left [\ mathrm {0,} t\ right]\ to {\ Omega} _ {t} ^ {i}\ subset} {\ mathrm {riam}} ^ {3}\\ & {3}\\ & {p} ^ {i}\ to {x} _ {t} ^ {i}\ mathrm {=} {\ varphi}} _ {\ varphi} _ {\ varphi} _ {\ varphi} _ {\ varphi} _ {\ varphi} _ {t}} _ {\ varphi} _ {t}} _ {\ varphi} _ {t}} _ {\ varphi} _ {t}} _ {\ varphi} _ {t}} _ {\ varphi} _ {t} ^ {i}\end{split}\]

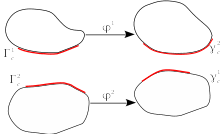
During their movement, solids may come into contact, as shown on the. The \({\Gamma }^{i}=\partial {\Omega }^{i}\) border of each solid \({B}^{i}\) is broken down into parts \({\Gamma }_{u}^{i}\), \({\Gamma }_{g}^{i}\), and \({\Gamma }_{c}^{i}\) in the initial configuration, whose intersections are empty two by two:

(2.2)\[ {\ Gamma} _ {u} ^ {i}\ mathrm {\ cap} {\ cap} {\ Gamma} _ {g} ^ {i}\ mathrm {=}\ mathrm {\ varnothing} {\ Gamma} _ {u} ^ {i}\ cap {\ Gamma} _ {c} ^ {i} =\ varnothing {\ Gamma} _ {c} ^ {i}\ cap {\ Gamma} _ {g} ^ {i} =\ varnothing {\ Gamma} _ {u} ^ {i}\ mathrm {\ cup} {\ cup} {\ Gamma} _ {g} ^ {i}\ mathrm {\ cup} {\ Gamma} _ {\ Gamma} _ {c} ^ {i} _ {c} ^ {i}\ mathrm {i}\ mathrm {=} {\ Gamma} ^ {i}\]

These borders are deformed in the current configuration in \({\gamma }_{u}^{i}\), \({\gamma }_{g}^{i}\), and \({\gamma }_{c}^{i}\). Solid \({B}^{i}\) is embedded on \({\Gamma }_{u}^{i}\) and subjected to a nominal density of surface forces noted \({g}^{i}\) on part \({\Gamma }_{g}^{i}\). Moreover, we note \({f}^{i}\) the field of volume density of forces applied to solids \({B}^{i}\). The parts of surfaces \({\Gamma }^{i}\) likely to come into contact during the deformation of the two solids are noted \({\Gamma }_{c}^{i}\). These surfaces are not known a priori (this is one of the non-linearities of the problem to be solved as will be seen later).

Figure 1 : Description of the different configurations of the mechanical problem

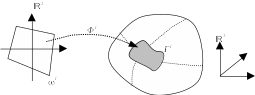
It is assumed the existence of regular maps marked \({\Phi }^{i}\) describing surfaces \({\Gamma }^{i}\). These maps are defined as follows:

(2.3)\[\begin{split} \ begin {array} {cc} {\ Phi} ^ {2}} ^ {i} (\ zeta) (\ zeta)\ mathrm {:} &\ omega\ mathrm {\ subset} {\ mathrm {\}}} ^ {2}\ to {\ omega} ^ {2}\ to {\ omega} ^ {2}\ to {\ omega} ^ {2}\ to {\ omega} ^ {2}\\\\ zeta ({\ zeta}}\ eta} _ {1}, {\ zeta} _ {2})\ to {p} ^ {i}\ mathrm {=} {\ Phi} ^ {i} (\ zeta)\ end {array}\end{split}\]

where \(\omega\) is a bounded (reference) domain contained in \({ℝ}^{2}\), see.

Figure 2 : Surface Description

The coordinates of the contact surfaces \({\Gamma }_{c}^{i}\) are transported by applying the deformation, at time \(t\) . They are therefore constructed by composition of the two functions:

\[\]

: label: eq-4

begin {array} {cc} {Phi} _ {t} ^ {i} _ {t} ^ {i} (zeta, t)mathrm {:} & {Gamma} _ {c} ^ {i}mathrm {times}\\\\\\\\\\\\\ left [mathrm {0,} ^ {i}\\\\\\\left [mathrm {0,} ^ {i}\\\\\\\ left [mathrm {0,} ^ {i}\\\\\\\ left [mathrm {0,} ^ {i}to {Phi} _ {t} ^ {i} (zeta)mathrm {=} {varphi} _ {t} ^ {i}mathrm {°} {Phi} {Phi} {Phi} ^ {i} (zeta)end {array}

The gradient tensor for transformation \(\underline{\underline{{F}_{t}^{i}}}\) is defined by:

\[\]

: label: eq-5

underline {underline {{F} _ {t}} ^ {i}}}}mathrm {=}frac {mathrm {partial} {x} _ {t} ^ {i}}} {mathrm {i}}} {mathrm {partial}} {p} ^ {i}}

If we denote by \({u}^{i}\) the field of movements of the solid \({B}^{i}\):

(2.4)\[ {x} _ {t} ^ {i} = {p} ^ {i} + {u} ^ {i} = {i}\]

Then the transformation gradient tensor is rewritten:

(2.5)\[ \ underline {\ underline {{F} _ {t}} ^ {i}}}}\ mathrm {=}\ mathrm {\nabla}\ mathrm {\ otimes} {u} {u} ^ {i}} +\ underline {\ underline {{i}}}}\]

Using function \({\varphi }_{t}^{i}\), we can write:

(2.6)\[ \ underline {\ underline {{F} _ {t} ^ {i}}}}\ mathrm {=}}\ frac {\ mathrm {\ partial} {\ varphi} _ {t} ^ {i} _ {t} ^ {i}} ({p} ^ {i}} ({p} ^ {i}} ({p} ^ {i}, t)} {\ mathrm {i}, t)} {\ mathrm {\ partial} {\ mathrm {i}}}\ mathrm {=} {\ mathrm {\nabla}} _ {{p} ^ {i}}}\ mathrm {\ otimes} {\ varphi} _ {t} ^ {i}\]

Where \(\mathrm{\otimes }\) is the tensor product and \({\mathrm{\nabla }}_{{p}^{i}}\) is the gradient operator (in space). The Jacobian for transformation is introduced:

(2.7)\[ {J} _ {t} ^ {i}\ mathrm {=}\ mathit {det} (\ underline {\ underline {{F} _ {t}} ^ {i}}}})\]

Note \(\overline{{\Omega }^{i}}\) the strict interior of \({\Omega }^{i}\) and \({\Gamma }^{i}\) its border:

(2.8)\[ {\ Omega} ^ {i} =\ overline {{\ Omega} ^ {i}}\ cup {\ Gamma} ^ {i}\]

2.1.1. Building local bases

The two applications \({\Phi }^{i}\) and \({\varphi }_{t}^{i}\) make it possible to define the local coordinate system on the solid \(i\). This local coordinate system is established by constructing the tangential plane at the point in question and therefore by the data of the two tangent vectors \({t}_{\alpha =\mathrm{1,2}}^{i}\) on the deformed configuration of the surface \({\gamma }^{i}\):

(2.9)\[ {t} _ {\ alpha} ^ {i} ({\ zeta}} _ {\ zeta} _ {c} ^ {i})\ mathrm {=}\ frac {\ partial} {\ Phi} {\ Phi} _ {t}} _ {\ zeta}} {\ zeta}}\ mathrm {=} {\ Phi} _ {\ Phi} _ {\ Phi} _ {t} ^ {i}}} {t} ^ {i}}} {\ frac {i}}} {\ mathrm {\ mathrm {\ mathrm} {\ partial} {\ varphi} _ {t} ^ {i} ({p} ^ {i}, t)} {\ mathrm {\ partial} {p} ^ {i}}}\ mathrm {.} \ frac {\ mathrm {\ partial} {\ partial} {\ Phi} {\ Phi} ^ {i} (\ zeta)} {\ mathrm {\ partial} {\ zeta}} _ {\ alpha}}\]

We can define the base vectors of the initial surface \({\Gamma }_{c}^{i}\) in the same way:

(2.10)\[ {T} _ {\ alpha} ^ {i} (\ zeta)\ mathrm {=}\ frac {\ mathrm {\ partial} {\ Phi} ^ {i} (\ zeta)} {\ zeta)} {\ mathrm {\ zeta}}\]

Using the definition of the transformation gradient tensor (), we explicitly express the relationship between \({T}_{\alpha }^{i}\) and \({t}_{\alpha }^{i}\):

(2.11)\[ {t} _ {\ alpha} ^ {i}\ mathrm {=}\ mathrm {=}\ underline {{F} _ {i} ^ {}}} {T} _ {\ alpha} _ {\ alpha} ^ {i}\]

There is no reason for \({t}_{\alpha }^{i}\) to be unitary and for the \(({t}_{1}^{i},{t}_{2}^{i})\) coordinate system to be orthogonal. We get the normals by simple vector product:

(2.12)\[ {n} ^ {i}\ mathrm {=}\ frac {{t}} _ {1} ^ {i}\ mathrm {\ times} {t} _ {2} ^ {i}} {{i}}} {{t}} _ {1} {t} _ {2} ^ {i}}} {t} _ {2} ^ {i}}} {i}} {t}} {\]

In Code_Aster, the normal is always obtained using the algorithm below:

• Calculation of tangent vectors on the current configuration;

• Modification of tangent vectors (according to options VECT_MAIT, VECT_ESCL);

• Calculation of the normal vector by vector product at the point in question.

By construction, tangent vectors \({t}_{\alpha }^{i}\) are orthogonal to normal \({n}^{i}\).

2.1.2. Regularization of local bases

It is sometimes necessary to use a field of « smoothed » normals to minimize the risks of instabilities of the contact problem when the surface is described by polynomial fields (typically the case of finite elements). For this, a very simple strategy has been implemented in the code (activable via option LISSAGE). The algorithm is described below:

• For each element \(e\) of the surface, for each node \(s\) of this element shared by \(k(s)\) elements, we calculate the normal unit \({n}^{e}(s)\) at this node \(s\);

• For each \(s\) node, we average \({n}_{L}(s)\) between the normals of each element sharing this common node:

(2.13)\[ {n} _ {L} (s) =\ frac {{\ sum} _ {{\ sum} _ {e=1} ^ {k\ left (s\ right)} {n} ^ {e}\ left (s\ right)} {{\ sum}} _ {\ sum} _ {e=1} _ {e=1} ^ {1} ^ {e}\ left (s\ right)} {\]

• The normal obtained by interpolation in accordance with the degree of the surface (linear or quadratic) is smoothed. If we designate the \(\mathit{nno}(e)\) shape functions of the element \(e\) by \({N}_{e}^{s}\), then the smoothed normal \({n}_{\text{lis}}(\overline{\zeta })\) at a point \(\overline{\zeta }\) of the element is simply written:

(2.14)\[ {n} _ {\ text {read}}\ left (\ overline {\ zeta}\ right) = {\ sum} _ {s=1} ^ {\ mathit {nno}\ left (e\ right)} {N} _ {e\ right)} {N} _ {e} ^ {s}\ left (\ overline {\ zeta}\ right)\ mathrm {.} {n} _ {L} (s)\]

Note: given that we take an unweighted arithmetic mean between the normals, if two adjacent elements are of very different sizes and normals, the smoothing obtained may be of poor quality.

2.1.3. Some remarkable identities

In this paragraph, we will present a number of remarkable identities relating to the properties of the \(({t}_{1},{t}_{2},n)\) database. First, let’s recall the definition of tangent vectors:

(2.15)\[ {t} _ {\ alpha}\ mathrm {=}\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ partial} {\ partial} {\ zeta}} _ {\ alpha}}\]

The vectors \({t}_{\alpha }\) and \(n\) are orthogonal to each other, so their dot product is zero:

(2.16)\[ {t} _ {\ alpha}\ mathrm {\ cdot} n\ mathrm {=} 0\]

The vector \(n\) is unitary by definition, its product by itself is a constant (which is equal to \(1\)):

(2.17)\[ n\ mathrm {\ cdot} n\ mathrm {=} 1\]

We define the matrix of the first fundamental form or metric tensor \(\underline{\underline{m}}\) whose components are:

(2.18)\[ {m} _ {\ alpha\ beta}\ mathrm {=} {t} _ {\ alpha}\ mathrm {\ cdot} {t} {t} _ {\ beta}\]

If the base was orthonormal, this tensor would be reduced to the identity tensor.

The inverse of the metric tensor is also the first fundamental form of dual space, its components equal:

\[\]

: label: eq-21

frac {1} {{m} _ {alphabeta}}}mathrm {=} {m} ^ {alphabeta}mathrm {=} {t} ^ {alpha}mathrm {alpha}mathrm {alpha}mathrm}mathrm {beta}} {beta}} {mathrm {partial} {zeta} ^ {alpha}}}mathrm {cdot}frac {mathrm {partial}overline {x}} {mathrm {partial}} {partial} {partial} {partial}} {partial} {partial}}

To pass tangent vectors from the covariant base to the contravariant base, we use the metric tensor [1] _ :

(2.19)\[ {t} ^ {\ alpha}\ mathrm {=} {m} ^ {\ alpha\ beta} {t} _ {\ beta}\]

With:

(2.20)\[ {m} _ {\ alpha\ beta} {m} {m} ^ {\ alpha\ beta}\ mathrm {=} 1\]

We also define the tensor of the second fundamental form, linked to curvature, whose components are as follows:

(2.21)\[ {\ kappa} _ {\ alpha\ beta}\ mathrm {=}\ mathrm {=}\ frac {{\ mathrm {\ partial}} ^ {2}\ overline {x}} {\ partial} {\ partial} {\ zeta} {\ zeta} _ {\ partial}}\ mathrm {\ cdot}} _ {\ beta}}\ mathrm {\ cdot} n\]

2.2. Kinematic non-interpenetration condition

To translate non-interpenetration, the procedure is as follows:

*We couple the points of the contact surfaces two by two: this is the*pairing; *

• A non-interpenetration condition is imposed between the two paired points in a given direction (generally the normal to one of the two surfaces at the point in question).

2.2.1. Pairing problem

By convention, the contact surface defined on solid \(1\) will be called slave surface and the paired surface defined on solid \(2\) will be called master surface. The pairing is performed by looking for, for any point \(x\) of the \({\gamma }_{c}^{1}\) border, the nearest point \(\overline{x}\) of \({\gamma }_{c}^{2}\). This is equivalent to solving the following minimization problem:

(2.22)\[ \ mathrm {\ forall} x\ mathrm {\ in} {\ in} {\ gamma} _ {c}\ text {and}\ mathrm {\ forall} t\ ge 0 {x} _ {t}\ mathrm {=} {=} {\ varphi} _ {t} ^ {1} ({p} ^ {1}, t) \ textrm {find} \ overline {\ zeta}\ mathrm {\ in}\ omega\ mathrm {\ times}\ left [\ mathrm {0,} t\ right] \ overline {\ zeta}\ mathrm {=}\ underset {\ zeta\ mathrm {\ in}\ omega} {\ text {argMin}}\ left\ {\ frac {1} {1} {2}\ mathrm {.} {{\ varphi} _ {t} ^ {1} ({\ Phi} ^ {1} (\ zeta), t)\ mathrm {-} {\ varphi} _ {t} ^ {2} ({\ Phi} ^ {2} ({\ Phi} ^ {2}) ^ {2}\ right\} (\ zeta), t)\]

Solution \(\stackrel{ˉ}{\zeta }\) is the position in the parametric reference space of the \(M\) projection of the projection of the slave node \(P\) onto the master mesh.

Figure 3 : Projection of the slave node onto the master mesh

Details of the implementation of the algorithm used for the matching problem are available in document [R5.03.50] (the matching method is strictly equivalent between the discrete methods and the continuous method).

2.2.2. Definition of the game

The pairing allows you to define the point \(\overline{p}\) of the surface \({\Gamma }_{c}^{2}\), paired with \(p\) at the moment \(t\) in the original configuration, and the point \(\overline{x}\) paired with \(x\) at the moment t in the current configuration. The distance vector \(d\) between the paired points is simply:

(2.23)\[ d\ mathrm {=} x\ mathrm {-}\ overline {x}\ overline {x}\ mathrm {=} {\ Phi} _ {t} ^ {1} (\ zeta)\ mathrm {-} {-} {\} {\ Phi}} _ {t} ^ {2} (\ overline {\ zeta})\]

This is the result of the minimization described in system ():

\[\]

: label: eq-27

overline {d}mathrm {=}underset {zetamathrm {in}omega} {mathit {min}}left{frac {1} {1} {2}mathrm {.} {{varphi} _ {t} ^ {1} ({Phi} ^ {1} (zeta), t)mathrm {-} {varphi} _ {t} ^ {2} ({Phi} ^ {2} ({Phi} ^ {2}) ^ {2}right} (zeta), t)

The first optimality condition is written as:

(2.24)\[ \ left [{\ Phi} _ {t} ^ {1} (\ zeta)\ mathrm {-} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta})\ right]\ right]\ mathrm {\ cdot} {1} (\ zeta)\ mathrm {\ cdot} {1} (\ zeta})\ mathrm {=} 0\]

With the definition of tangent vectors on the deformed surface \({\gamma }_{c}^{2}\):

(2.25)\[ {t} _ {\ alpha} (\ overline {\ zeta})\ mathrm {\ zeta})\ mathrm {=}\ frac {\ mathrm {\ zeta}} {\ overline {\ zeta}}\ mathrm {\ zeta}}\ frac {\ mathrm {\ partial} {\ partial}}} {\ mathrm {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ zeta}} _ {\ zeta} _ {\ alpha}}\ mathrm {=}\ frac {\ mathrm {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ zeta}} {t} ^ {2}} {\ mathrm {\ partial}\ overline {p}}\ mathrm {.} \ frac {\ mathrm {\ partial} {\ partial} {\ Phi}} {\ Phi} ^ {2} (\ overline {\ zeta})} {\ mathrm {\ partial} {\ zeta}} _ {\ alpha}}\]

We can go back to the basic vectors of the initial surface \({\Gamma }_{c}^{2}\):

\[\]

: label: eq-30

{T} _ {alpha} ({overline {zeta}}} _ {t})mathrm {=}frac {mathrm {partial} {Phi} {Phi} ^ {2} ({overline {zeta}} ({zeta}} ({overline {zeta}} ({zeta}} ({zeta}}) {overline {zeta}} ({zeta}} ({overline {zeta}}) _ {zeta}} ({overline {zeta}} ({zeta}}) {overline {zeta}} ({zeta}} ({

Using the definition of the transformation gradient tensor, we explicitly express the relationship between \({T}_{\alpha }\) and \({t}_{\alpha }\):

\[\]

: label: eq-31

{t} _ {alpha}mathrm {=}mathrm {=}underline {underline {{F} _ {2} ^ {}}}} {T}} {T} _ {alpha}

We get the normal by simple vector product:

\[\]

: label: eq-32

n ({overline {zeta}} _ {t})mathrm {=}frac {{t} _ {1}mathrm {times} {t} _ {2}}} {mathrm {parallel}}} {mathrm {parallel} {t}}} {mathrm {parallel} {t}}

The base constructed by the three vectors \(({t}_{1},{t}_{2},n)\) has no a priori reason to be orthonormal. On the other hand, by construction, the normal \(n\) is unitary and normal to the plane defined by the vectors \(({t}_{1},{t}_{2})\) which define the tangential plane to the deformed surface \({\gamma }_{c}^{2}\). By using equality () we necessarily have:

(2.26)\[ \ left [{\ Phi} _ {t} ^ {1} (\ zeta) (\ zeta)\ mathrm {-} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta})\ right]\ right]\ right]\ mathrm {=} {d} _ {n} n\]

\({d}_{n}\) is a signed algebraic quantity. Like \(x\mathrm{=}{\Phi }_{t}^{1}(\zeta )\), we get:

(2.27)\[ x\ mathrm {=} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta}) + {d} _ {n} n\]

\({d}_{n}\) is called game between the two solids at point \(x\). This gives us the relationship between the base \(({t}_{1}^{1},{t}_{2}^{1},{n}^{1})\) defined on the tangential plane at the slave point and the base \(({t}_{1},{t}_{2},n)\) built by the projection of the point \(x\) onto the deformed surface (master) \({\gamma }_{c}^{2}\):

(2.28)\[ {t} _ {\ alpha} ^ {1} (\ overline {\ zeta})\ mathrm {=} {t} _ {\ alpha} (\ overline {\ zeta}) + {d} _ {n}\ n}\ frac {\ mathrm {\ zeta})\ frac {\ mathrm {\ zeta}} (\ overline {\ alpha}}} (\ overline {\ alpha}}} (\ overline {\ alpha}}) zeta}) {n} ^ {1}\ mathrm {=} n\]

The two frames of reference are coincident if the points are in contact (if \({d}_{n}=0\)). The distance is divided into a normal part \({d}_{n}\) and a tangential part \({d}_{\tau }\):

(2.29)\[ d\ mathrm {=} {d} _ {n} n+ {d} _ {\ tau}\]

For the expression for \({d}_{\tau }\), we get:

(2.30)\[ {d} _ {\ tau}\ mathrm {=}} {\ underline {\ underline {\ underline {{P} _ {}}}} ^ {\ tau} d\ mathrm {=} {\ underline {\ underline {\ underline {\ underline {\ underline {{{P} {{P} _ {}}}}} ^ {\ tau}}} ^ {\ tau} (x\ mathrm {-}}\ overline {x})\]

With \({\underline{\underline{{P}_{}}}}^{\tau }\) the tangential plane projection matrix:

(2.31)\[ {\ underline {\ underline {{P} _ {}}}}}} ^ {\ tau}\ mathrm {=}\ underline {\ underline {{I} _ {}}}\ mathrm {-}}\ mathrm {-}\ underline {-}\ underline {}}\ underline {\ underline {{n}} _ {}}}\]

We can write the non-interpenetration condition between \(x\mathrm{\in }{\gamma }_{c}^{1}\) and \(\overline{x}\mathrm{\in }{\gamma }_{c}^{2}\) according to the search direction \(n\mathrm{=}\mathrm{-}{n}^{2}(\overline{x})\), normal incoming unit at point \(\overline{x}\) (directed towards the inside of \({\Omega }_{t}^{2}\)):

(2.32)\[ {d} _ {n}\ mathrm {=} (x\ mathrm {-}\ overline {x})\ mathrm {\ cdot} n\ mathrm {\ the} 0\]

This quantity is objective.

Note:

Given the choice of normal, the game is « reversed » compared to the case of contact in discrete formulation in*Code_Aster: there is interpenetration if \({d}_{n}\mathrm{\ge }0\);

2.2.3. Relative speed

To write Coulomb’s law of friction, we’ll need the concept of the relative sliding speed between the two solids. To do this, we use the definition of the normal game ():

(2.33)\[ \ left [{\ Phi} _ {t} ^ {1} (\ zeta) (\ zeta)\ mathrm {-} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta})\ right]\ right]\ right]\ mathrm {=} {d} _ {n} n\]

We start by differentiating the term on the right with respect to time:

(2.34)\[ \ frac {d} {\ mathit {dt}}}\ left ({d} _ {n} n\ right) =\ dot {{d} _ {n}} n+ {d} _ {n}\ left (\ frac {\ partial n}} {\ partial n} {\ partial t} +\ frac {\ partial t} +\ frac {\ partial t} +\ frac {\ partial n} {\ partial n} {\ overline {{\ mathrm {\ zeta}}\ left (\ frac {\ partial n}}\ left (\ frac {\ partial n}} {\ partial n} +\ frac {\ partial n}} +\ frac {\ partial n} {\ partial n} {\ overline {{\ mathrm {\ zeta}}\ left mathrm {\ alpha}}}}}\ frac {\ partial\ overline {{\ mathrm {\ zeta}}} ^ {\ mathrm {\ alpha}}}}} {\ partial t}\ right)\]

With the usual summation convention on silent indices \(\alpha\). Then we derive the term from the left:

(2.35)\[\begin{split} \ frac {d} {\ mathit {dt}} ({\ Phi}}} ({\ Phi}} _ {\ Phi}}} (\ Phi} _ {t} ^ {2} (\ overline {\ zeta})) (\ overline {\ zeta}))\ mathrm {\ zeta}))\ mathrm {=}\ frac {\ mathrm {\ partial} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta}) (\ overline {\ zeta}))\ mathrm {=}}\ frac {\ mathrm {\ partial} {\ Phi} _ {t} ^ {2} (\ overline {\ zeta}) (\ overline {\ zeta}))\\ mathrm {\ partial} t}\ mathrm {-}\ frac {\ mathrm {\ partial} {\ Phi} _ {t} ^ {2}} {\ mathrm {\ partial} t}\ mathrm {-}\ frac {\ mathrm {-}}\ frac {\ mathrm {-}}\ frac {\ mathrm {\ partial}}\ frac {\ mathrm {\ partial}}\ frac {\ mathrm {\ partial}\ overline {{\ zeta} ^ {\ alpha}}}}}\ frac {\ mathrm {\ partial}\ overline {{\ zeta}} ^ {\ alpha}}}} {\ mathrm {\ partial} t}\end{split}\]

We recognize the definition of \({t}_{\alpha }\) in the term \(\frac{\mathrm{\partial }{\Phi }_{t}^{2}}{\mathrm{\partial }{\zeta }_{\alpha }}\) (see ()). We equal the two terms () and ():

(2.36)\[ \ dot {{d} _ {n}}\ text {.} n+ {d} _ {n}\ text {.} (\ frac {\ mathrm {\ partial} n} {\ mathrm {\ partial} n}} {\ mathrm {\ partial} n} {\ mathrm {\ partial}\ overline {\ partial}\ overline {\ zeta}} ^ {\ zeta}} ^ {\ alpha}}}\ mathrm {.} \ frac {\ mathrm {\ partial}\ overline {\ zeta}} {\ mathrm {\ partial} t})\ mathrm {=}\ frac {\ mathrm {\ partial} {\ partial} {\ Phi} {\ Phi} _ {\ Phi} _ {t} ^ {1}}} {\ mathrm {\ partial} t})\ mathrm {-}\ frac {\ partial} {\ partial} {\ Phi} _ {t} ^ {1}}} {\ mathrm {\ partial} t}\ mathrm {-}\ frac {\ partial} {\ partial} {\ Phi}} _ {t} ^ {1}} {\ mathrm {\ partial} {\ Phi} _ {t} ^ {2}}} {\ mathrm {\ partial} t}\ mathrm {-}\ frac {\ mathrm {\ partial}\ overline {{\ zeta}} _ {\ zeta}} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ alpha}\]

Assuming \(v(x,t)\) the speed of point \(x\) and \(\overline{v}(\overline{x},t)\) the speed of the paired point \(\overline{x}\):

(2.37)\[ v (x, t)\ mathrm {=}\ frac {\ mathrm {\ partial} {\ Phi} _ {t} ^ {1}}} {\ mathrm {\ partial} t}\]

We finally get using ():

(2.38)\[\begin{split} \ dot {{d} _ {n}} n+ {d}} _ {d} _ {n}\ frac {\ mathrm {\ partial} t}} +\ frac {\ mathrm {\ partial}\ frac {\ mathrm {\ partial}\ partial}\\ partial}\\ partial}\\\ partial} +\ frac {\ mathrm {\ partial} t} {\ mathrm {\ partial} t} {\ partial} {\ partial} t} {\ partial}\} ^ {1}\ mathrm {=} {v} {v} ^ {1}\ mathrm {-}\ overline {v}\end{split}\]

Note \({v}_{\text{gliss}}\) the sliding speed:

(2.39)\[ {v} _ {\ text {gliss}}\ mathrm {=} v\ mathrm {-} (\ stackrel {} {v} + {d} _ {n}\ frac {\ mathrm {\ partial} n} {\ mathrm {\ partial} n} {\ mathrm {\ partial} t})\]

This quantity is objective because it is invariant by change of frame of reference. The relative sliding speed is identified with the difference in the speed of the two solids, only when they are in contact (\({d}_{n}\mathrm{=}0\)).

2.2.4. Discontinuity operator

We note \(\mathrm{〚}g\mathrm{〛}(p)\) the discontinuity of the quantity \(g\) between the solid \(1\) and the solid \(2\). This discontinuity is written at the point \(p\) on \(1\) which is projected to \(\stackrel{ˉ}{p}\) on \(2\) depending on the pairing application:

(2.40)\[ \ mathrm {} g (p)\ mathrm {}\ mathrm {}\ mathrm {=} {g} ^ {2}\ mathrm {-} {g} ^ {2} (\ overline {p})\]

Subsequently we will abandon the notation \(\mathrm{〚}g(p)\mathrm{〛}\) in favor of \(\mathrm{〚}g\mathrm{〛}\) by making the implicit assumption that the discontinuity is written on the pair \((p,\overline{p})\) of the paired points. We can decompose this discontinuity into a normal part \({\mathrm{〚}g\mathrm{〛}}_{n}\) and a tangential part \({\mathrm{〚}g\mathrm{〛}}_{\tau }\):

(2.41)\[ \ mathrm {} g\ mathrm {}\ mathrm {}\ mathrm {} g\ mathrm {}} _ {n} n+ {\ mathrm {}}\ mathrm {} g\ mathrm {}} _ {\ tau}\]

With:

(2.42)\[ {\ mathrm {} g\ mathrm {}}} _ {n}\ mathrm {=}\ mathrm {} g\ mathrm {}\ mathrm {}\ mathrm {\ cdot} n\]

Where \(n\) is the normal to the master surface, directed toward the inside of solid \(2\).

The tangential part:

\[\]

: label: eq-50

{mathrm {} gmathrm {}}} _ {tau}mathrm {=} {underline {underline {{P} _ {}}}}} ^ {tau}}}} ^ {tau}mathrm {}}} ^ {tau}mathrm {}}} ^ {tau}mathrm {}}

With the notations introduced, game \({d}_{n}\) can be written as:

(2.43)\[ {d} _ {n}\ mathrm {=} {\ mathrm {}} x\ mathrm {}} _ {n}\ mathrm {=} {\ mathrm {}} p+u\ mathrm {}} _ {n}\]

It should be noted that the quantities projected onto the normal are necessarily scalar, hence the notation in \({\mathrm{〚}g\mathrm{〛}}_{n}\) and not in \({\mathrm{〚}g\mathrm{〛}}_{n}\).

2.3. Variations in kinematic quantities

The contact surfaces are described by a set of four parameters \(({\zeta }_{1}^{1},{\zeta }_{2}^{1},{\zeta }_{1}^{2},{\zeta }_{2}^{2})\), in the reference space (parametric) of the finite elements. The master/slave approach makes it possible to reduce this number by describing kinematic variables \(\zeta\) in relation to a body taken as a reference (in this case, the body defined as « master »). The adequate choice of the reference surface is not an immediate step and remains a modeling hypothesis to be taken into consideration, especially in cases of a large relative slippage of the two surfaces. It is necessary to distinguish Lagrangian derivatives from Eulerian derivatives. The purpose of this paragraph is to assess the various variations. We define the variation \(\delta f({x}_{0})\) from a function \(f(x)\) to a variable at a given point \({x}_{0}\) by the quantity:

\[\]

: label: eq-52

delta f ({x} _ {O})mathrm {=}underset {delta xto 0} {mathit {lim}} (f ({x} _ {0} + {delta} _ {0} + {delta} _ {O}) + {delta} _ {O}) + {delta} _ {0}) + {delta} _ {0}) + {delta} _ {0}) + {delta} _ {x} _ {x})mathrm {-} f ({x} _ {0}))mathrm {frac {mathrm {x} {x}})mathrm {partial} f} {mathrm {partial} x}}mathrm {mid}} _ {{x} _ {0}}}delta x

In the case of a function with several variables, a distinction is made between the total variation (with respect to all its variables), noted \(\tilde{\delta }f\), and the partial variation with respect to a variable \(x\), noted \({\delta }_{x}f\). The total change is the sum of all partial changes. Note \(\tilde{\delta }\) the total variation of a kinematic quantity. If we write the time variable \(t\), we will have, in the case of an Eulerian quantity \(\stackrel{ˉ}{a}\):

(2.44)\[ \ tilde {\ delta}\ stackrel {} {a}\ mathrm {=}\ frac {\ mathrm {\ partial}\ stackrel {} {a}} {\ mathrm {\ partial} t}\ delta t+\ delta t+\ frac {\ mathrm {\ partial}\ stackrel {} {a}} {\ mathrm {\ partial}} {\ mathrm {\ partial}} {\ mathrm {\ partial} t}\ delta t+\ frac {\ mathrm {\ partial}} {\ zeta} _ {\ alpha}}\ delta {\ zeta} ^ {\ alpha}\]

It is therefore the sum of a variation \({\delta }_{t}\) with respect to time \(t\) and the variation \({\delta }_{\zeta }\) with respect to parametric coordinates:

(2.45)\[ \ tilde {\ delta}\ stackrel {} {a} {a}\ mathrm {=} {\ delta} _ {t}\ stackrel {} {a} + {\ delta} _ {{\ zeta} _ {\ zeta}} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta} _ {\ zeta\]

If we now consider a Lagrangian quantity \(a\), its variation with respect to the parametric coordinates \(\zeta\) is zero:

(2.46)\[ \ tilde {\ delta} a\ mathrm {=} {\ delta}} _ {\ delta} _ {\ delta} _ {\ zeta} _ {\ alpha}}} a\ mathrm {=} 0\]

The quantities linked to the slave surface are Lagrangian quantities, those related to the master surface are Eulerian quantities.

2.3.1. Weingarten’s formulas

First, we use the fact that the variation of a constant is zero regardless of the parameter that varies. Now according to () the product \((n\mathrm{\cdot }n)\) is constant, so:

(2.47)\[ \ frac {1} {2}\ delta (n\ mathrm {\ cdot} n)\ mathrm {=} 0\]

Expanding () we get:

(2.48)\[ \ delta n\ mathrm {\ cdot} n\ mathrm {=} 0\]

The product is zero if, and only if, \(\delta n\) is orthogonal to \(n\), and therefore \(\delta n\) belongs to the tangential plane:

(2.49)\[ \ delta n\ mathrm {=} a {t} _ {1} +b {t} _ {2} \ mathrm {\ forall} a, b\ mathrm {\ in}\ mathrm {\ in}\ mathrm {\ times}\ mathrm {\ in}\ mathrm {\ in}\ mathrm {\ in}\ mathrm {\ in}\ mathrm {\]

Note that the variation of the normal belongs to the tangential plane, using constants \({c}_{\beta }\):

(2.50)\[ \ delta n\ mathrm {=} {c} _ {\ beta} {t} _ {\ beta} \ mathrm {\ forall} {c} _ {\ beta} _ {\ beta}\ mathrm {\ in}\ mathrm {zzy}\]

We are now going to establish some very practical formulas that we will need later. The first thing to do is to give the formula establishing the value of the coefficients \({c}_{\beta }\). We start by establishing the following dot product:

(2.51)\[ \ delta n\ mathrm {\ cdot} {t} {t} _ {\ alpha} _ {\ alpha}\ mathrm {=} {c} _ {\ beta}\ mathrm {\ cdot} {t} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _ {\ alpha} {t} _\]

Then, we start with the property ():

(2.52)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot}} n\ mathrm {\ cdot} n\ mathrm {=} 0\]

We calculate its first variation, the variation of a constant is zero regardless of the parameter that varies:

\[\]

: label: eq-62

delta (frac {mathrm {partial}overline {x}} {mathrm {partial} {zeta} _ {alpha}})mathrm {cdot} n+frac {mathrm {partial}overline {partial}} {mathrm {partial}} {zeta} n+frac {mathrm {partial}}mathrm {zeta} n+frac {mathrm {partial}}mathrm {zeta} n+frac {mathrm {partial}} {cdot}delta nmathrm {=} {=} 0tofrac {mathrm {partial}overline {x}} {mathrm {partial} {zeta} {zeta} _ {alpha}} _ {alpha}}}mathrm {alpha}}}mathrm {alpha}}}mathrm {mathrm {-}delta (frac {mathrm {-}delta (frac {mathrm {-}}delta (frac {mathrm {-}}delta (frac {mathrm {-}) m {partial}overline {x}} {mathrm {partial} {partial} {partial} {zeta} _ {alpha}})mathrm {cdot} nmathrm {=}mathrm {=}mathrm {-} {-} {kappa} _ {alphabeta}

We find the components of the second fundamental form, to the nearest sign. By identifying with (), we have the following relationship:

(2.53)\[ {c} _ {\ beta} {m} _ {\ alpha\ beta}\ mathrm {=}\ mathrm {-} {\ kappa} _ {\ alpha\ beta}\ to {c} _ {\ beta}\ {\ beta}\ mathrm {=}\ mathrm {=}}\ mathrm {=}}\ mathrm {-} {m} ^ {\ alpha\ beta} {\ kappa} _ {\ alpha\ beta} _ {\ beta} _ {\ beta}\ mathrm {=}\ mathrm {=}}\ mathrm {-} {m} ^ {\ alpha\ beta} {\ kappa} _ {\ beta} _ {\ beta} _ {\ beta}\ mathrm {=}}\]

The normal variation is therefore equal to:

(2.54)\[ \ delta n\ mathrm {=}\ mathrm {-} {m} {m} ^ {\ alpha\ beta} {\ kappa} _ {\ alpha\ beta} {t} _ {\ beta}\]

By applying (), we have:

(2.55)\[ \ delta n\ mathrm {=}\ mathrm {-} {\ kappa} _ {\ alpha\ beta} {t} ^ {\ alpha}\]

Using (), we have:

(2.56)\[ \ delta n\ mathrm {=}\ mathrm {-} (\ delta (\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta}} {\ zeta}} _ {\ zeta} _ {\ alpha}} _ {\ alpha}})\ mathrm {\ cdot}})\ mathrm {\ cdot} n)\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ partial} {\ zeta}} {\ zeta} _ {\ alpha}} _ {\ alpha}})\ mathrm {\ cdot}} n)\ frac {\ mathrm {\ partial}} {\ partial} {\ partial} m {\ partial} {\ zeta} ^ {\ alpha}}\]

It’s Weingarten’s formula.

2.3.2. Variation of the normal game

From the definition of normal play ():

(2.57)\[ x\ mathrm {-}\ overline {x}\ mathrm {=} {d} _ {n} n\]

The first total variation is applied:

(2.58)\[ \ tilde {\ delta} x\ mathrm {=}\ tilde {\ delta}\ tilde {\ delta} +\ tilde {\ delta} {d} _ {n} n+ {d} {d} _ {d} _ {n} _ {n}\ tilde {\ delta} n\]

By definition \(\overline{x}\) is an Eulerian quantity, its variation is therefore expressed by the formula ():

(2.59)\[ \ tilde {\ delta}\ overline {x}\ mathrm {=} {\ delta} _ {t}\ overline {x} +\ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {x}}} {\ mathrm {\ partial}} {\ partial}} {\ partial}} {\ alpha}}\ delta {\ zeta} ^ {\ alpha}}\ delta {\ zeta} ^ {\ alpha}}\]

Likewise for the change in normal:

(2.60)\[ \ tilde {\ delta} n\ mathrm {=} {\ delta} _ {\ delta} _ {t} n+\ frac {\ mathrm {\ partial} {\ partial} {\ zeta} {\ zeta}} _ {\ zeta} _ {\ delta}} _ {\ alpha}} _ {\ alpha}}\ delta {\ zeta} ^ {\ alpha}\]

Since \(x\) is a Lagrangian quantity, \(\tilde{\delta }x\mathrm{=}{\delta }_{t}x\). Finally:

\[\]

: label: eq-71

{delta} _ {t} xmathrm {=} {partial} {=} {delta} _ {t}overline {x} +frac {mathrm {partial}} {mathrm {partial}} {partial} {partial} {partial} {partial}} {partial}}} {partial}}} {mathrm {partial}}} {partial}}} {mathrm {partial}}} {partial}}} {mathrm {partial}}} {partial}}} {mathrm {partial}}} {partial}}} {mathrm {partial}}} {partial}}} {mathrm {partial}}} {partial}} {n} n+ {d} _ {n} ({delta}} _ {delta} _ {t} n+frac {mathrm {partial} {partial} {zeta} {zeta} _ {zeta} _ {alpha}} _ {alpha}} _ {alpha}} _ {alpha}} _ {alpha}} _ {alpha}}delta {zeta}}

If we make the product of this identity with the normal \(n\):

(2.61)\[ {\ delta} _ {t} x\ mathrm {\ cdot} n\ mathrm {\ cdot} n\ mathrm {\ cdot} n +\ delta {\ zeta} n +\ delta {\ zeta} ^ {\ zeta} ^ {\ zeta} ^ {\ alpha}\ frac {\ alpha}\ frac {\ mathrm {\ partial}}\ overline {x}} {\ mathrm {\ partial}} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot} n+\ tilde {\ delta} {d} {d} _ {n} n\ mathrm {\ cdot} n+ {d} _ {n} ({\ delta} _ {t} n+\ delta {\ t} n+\ delta {\ zeta} n+\ delta {\ zeta}} ^ {\ alpha}\ frac {\ mathrm {\ partial} n} {\ partial} n} {\ mathrm {\ partial} n} ({\ delta} _ {n} ({\ delta} _ {t} n+\ delta} _ {t} n+\ delta {\ zeta} n+\ delta {\ zeta}} ^ {\ alpha}\ frac {\ mathrm {\ partial} n} partial} {\ zeta} _ {\ alpha}})\ mathrm {\ cdot} n\]

We consider the properties (), () and (), that is to say:

(2.62)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot}} n\ mathrm {\ cdot} n\ mathrm {=} 0\]

This simplifies the expression:

(2.63)\[ \ tilde {\ delta} {d} _ {n}\ mathrm {=} {=} n\ mathrm {\ cdot} ({\ delta} _ {t} x\ mathrm {-} {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {n} _ {n} _ {n}\]

The first variation of the game does not lead to the appearance of transport terms (as in the equation). So \({d}_{n}\) is a purely Lagrangian quantity.

2.3.3. Variation of parametric coordinates

We start with the first variation of the expression () (taking into account the fact that \({d}_{n}\) is a Lagrangian quantity):

(2.64)\[ {\ delta} _ {t} x\ mathrm {=} {\ partial} {\ delta} _ {t}\ overline {x} +\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial}} {\ partial} {\ partial}} {\ partial}} {\ partial}}} {\ mathrm {\ partial}}} {\ mathrm {\ partial}}} {\ partial}} {\ mathrm {\ partial}}} {\ partial}} {\ mathrm {\ partial}}} {\ partial}} {\ mathrm {\ partial}}} {\ partial}} {\ mathrm {\ partial}}} {\ partial}} {\ mathrm {\ partial}}} {\ partial}} d} _ {n} ({\ delta} _ {t} n+\ frac {\ mathrm {\ partial} n} {\ mathrm {\ partial} {\ zeta}} _ {\ alpha}} _ {\ alpha}}}\ delta {\ alpha}}}\ delta {\ zeta} ^ {\ alpha})\]

This time we multiply this time by \(\frac{\mathrm{\partial }\overline{x}}{\mathrm{\partial }{\zeta }_{\beta }}\):

(2.65)\[\begin{split} {\ delta} _ {t} x\ mathrm {\ cdot}\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta}} _ {\ beta}} _ {\ beta}}}\ mathrm {}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}}}\ mathrm {\ beta}} {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ partial} {\ partial} {\ partial} {\ zeta} + (\ delta {\ zeta} ^ {\ alpha}\ frac {\ mathrm {\ partial}}\ overline {\ partial}\\ partial}} {\ partial}} {\ partial}} + (\ delta {\ zeta}} ^ {\ alpha}}\ frac {\ mathrm {\ partial}}\ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ partial} {\ zeta}} _ {n} n\ mathrm {\ cdot}\ frac {\ mathrm {\ cdot}\ frac {\ mathrm {\ partial}} {\ mathrm {\ partial}} {\ partial} {\ partial} {\ zeta}} {\ partial} {\ zeta}} {\ zeta} _ {beta} {\ beta} {\ beta}} {\ mathrm {\ partial} {\ partial} {\ zeta}}}} + {d} _ {n} ({\ delta}} _ {t} n\ mathrm {\ cdot}\ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ partial} {\ zeta}} + (\ delta {\ zeta} ^ {\ alpha}\ frac {\ alpha}\ frac {\ mathrm {\ partial}}} {\ partial} n} {\ mathrm {\ partial} n} {\ partial} n} {\ partial} n} {\ mathrm {\ partial} n} {\ partial} n} {\ mathrm {\ partial} n} {\ partial} n} {\ mathrm {\ partial} n} {\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ beta}})\end{split}\]

We find the metric tensor \(\underline{\underline{m}}\) whose covariant components are equal to:

(2.66)\[ {m} _ {\ alpha\ beta}\ mathrm {=} {t} _ {\ alpha}\ mathrm {\ cdot} {t} {t} _ {\ beta}\]

If we consider the property (), that is to say:

(2.67)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot}} n\ mathrm {\ cdot} n\ mathrm {=} 0\]

The expression is simplified:

(2.68)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ beta}}\ mathrm {\ cdot} ({\ delta} _ {t} _ {t} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} {d} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} x\ mathrm {-} {n}\ delta} _ {t} n\ mathrm {\ cdot}\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ beta}}\ {\ beta}}\ mathrm {}}\ mathrm {=}\ mathrm {=}}\ delta {\ zeta}} ^ {\ alpha}} ({m} _ {beta}} + {\ beta} _ {\ beta}}}\ mathrm {=}\ mathrm {=}\ delta {\ zeta}} frac {\ mathrm {\ partial} n} {\ mathrm {\ partial} {\ partial} {\ partial} {\ partial}} {\ mathrm {\ partial}\ frac {\ mathrm {\ partial}\ overline {\ partial}\ overline {x}}} {\ mathrm {\ partial}} {\ partial}} {\ partial}} {\ partial}} {\ partial}} {\ mathrm {\ partial}})\]

We start from the expression () that we will differentiate:

(2.69)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot} n\ mathrm {=} =} 0\ to\ frac {\ frac {\ partial}} {\ mathrm {\ partial}} {\ zeta} _ {\ beta}} _ {\ beta}} (\ frac ac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot} n)\ mathrm {\ cdot} n)\ mathrm {=} 0\]

By developing:

\[\]

: label: eq-81

frac {mathrm {partial}} {mathrm {partial} {partial} {partial} {partial}} {mathrm {partial}overline {x}} {mathrm {partial}} {partial} {partial} {partial} {zeta} {zeta}} _ {beta}}} (frac {mathrm {partial}}overline {x}}} {frac}} {frac {mathrm {partial}} ^ {2}overline {x}}} {mathrm {partial} {zeta} _ {alpha}mathrm {partial} {zeta} {zeta}} _ {zeta} _ {beta} _ {beta}} _ {beta}}}mathrm {cdot}} n+mathrm {cdot} n+frac {mathrm {partial}overline {x}} {zeta}} {zeta}} {zeta}} {mathrm {partial}} {zeta} {partial} {zeta} _ {alpha}}mathrm {cdot}}frac {mathrm {partial} n} {mathrm {partial} {zeta} {zeta} _ {beta}}}{beta}}}{beta}}{beta}}mathrm {beta}}mathrm {beta}}mathrm {=} 0tofrac {partial}overline {x}} {mathrm {partial}} {mathrm {partial}} {mathrm {partial}} {zeta} _ {alpha}}mathrm {cdot}frac {mathrm { partial} n} {mathrm {partial} {partial} {zeta} {zeta} _ {beta}}mathrm {-}frac {{mathrm {partial}}} ^ {2}overline {x}} {zeta}} {mathrm {partial}} {zeta} _ {alpha}mathrm {partial}}} ^ {2}overline {x}}} {overline {x}} {zeta} {zeta} _ {alpha}mathrm {partial}} {partial}} ^ {2}overline {x}}} {zeta} {zeta}} _ {beta}}mathrm {cdot} n

It is the curvature tensor () to the nearest sign. To find \(\delta {\zeta }^{\alpha }\), you need to solve the following system:

\[\]

: label: eq-82

{C} _ {alphabeta}delta {zeta}delta {zeta} ^ {alpha}mathrm {=} {B} _ {beta}

With:

\[\]

: label: eq-83

{C} _ {alphabeta}mathrm {=} ({m} _ {alphabeta}mathrm {-} {d} _ {n} {kappa} _ {kappa} _ {alphabeta})

2.3.4. Variation of tangents

Since \({t}_{\alpha }\) is an Eulerian quantity, we apply () to ():

(2.70)\[ \ tilde {\ delta} {t} _ {\ alpha}\ mathrm {=}\ tilde {\ delta} (\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial}} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial}} {\ partial} {\ partial}} {\ partial} {\ partial}} {\ partial} {\ partial}} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {\ partial} {t}\ overline {x})} {\ mathrm {\ partial} {\ partial} {\ partial} {\ partial} {\ partial}} +\ frac {{\ mathrm {\ partial}} ^ {2}\ overline {x}}} {\ overline {x}}}} {\ mathrm {\ partial}}} {\ partial}} ^ {2}\ overline {x}}}} {\ overline {x}}}} {\ overline {x}}} {\ partial}} {\ partial}} {\ partial}}\ delta {\ zeta} ^ {\ beta}\]

2.3.5. Second variation of the normal game

The second variation will be noted \(\Delta \delta\) in order to maintain the distinction between Lagrangian and Eulerian derivatives (and the notation \(\stackrel{}{˜}\)). To calculate the second variation of the normal game, we do not start from the expression () but directly from ():

(2.71)\[ {d} _ {n} n\ mathrm {=} (x\ mathrm {-}\ overline {x})\]

The first variation of the term on the right of () is equal to:

(2.72)\[\begin{split} \ tilde {\ delta} (x\ mathrm {-}\ overline {-}\ overline {x})\ mathrm {-}\ mathrm {-} {\ delta} _ {t}\ overline {x}\ overline {x}\ overline {x}}\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {\ partial}\ overline {x}} {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {t} _ {t} _ {t}\\ delta} _ {t} _ {t}\\ overline {x} _ {\ delta} _ {\ delta} _ {t}} {\ zeta} _ {\ alpha}}}\ delta {\ zeta} ^ {\ alpha})\end{split}\]

We will now calculate the second (total) variation by applying the operator \(\tilde{\Delta }\) on (). First, we use the fact that \({\delta }_{t}x\) is a Lagrangian quantity, so we have:

\[\]

: label: eq-87

tilde {Delta} {delta} _ {t} xmathrm {=} {Delta} _ {delta} _ {delta} _ {t} x

On the other hand, \({\delta }_{t}\overline{x}\) is an Eulerian quantity:

\[\]

: label: eq-88

tilde {Delta} {delta} _ {t}overline {x}overline {x}mathrm {=} {delta} _ {t}overline {x} +frac {mathrm {partial}frac {mathrm {partial}} ({mathrm {partial} {zeta}} _ {t}overline {x})} {mathrm {partial} {zeta} _ {alpha}}Delta {zeta} ^ {alpha}

Second variation of the convective term of ():

(2.73)\[ \ tilde {\ Delta} (\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ delta {\ zeta}} ^ {\ zeta} ^ {\ alpha} ^ {\ alpha})\ mathrm {\ partial} ^ {\ alpha})\ mathrm {\ alpha})\ mathrm {\ alpha})\ mathrm {=}\ tilde {\ Delta} (\ frac {\ mathrm {\ partial}}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}})\ delta {\ zeta}} ^ {\ alpha} +\ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial}} {\ alpha}})\ delta {\ partial}} {\ alpha}}\ tilde {\ delta}\ delta {\ zeta}\ overline {x}}}} {\ mathrm {\ partial}}} {\ mathrm {\ partial}}} {\ mathrm {\ partial}}} {\ mathrm {\ partial}} {\ alpha}} {\ mathrm {\ partial}} {\ alpha}} {\ mathrm {\ partial}} {\ alpha}}\]

So, the second variation of () is equal to:

(2.74)\[ \ tilde {\ Delta}\ tilde {\ delta} (x\ mathrm {-}\ mathrm {-}\ overline {x})\ mathrm {=} ({\ Delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {t}\ overline {x} _ {\ delta} _ {t}\ mathrm {-}\ frac\ mathrm {\ partial} ({\ delta} _ {t}\ overline {x})} {\ mathrm {\ partial} {\ zeta}}\ Delta {\ zeta}}\ Delta {\ zeta} ^ {\ alpha} ^ {\ alpha}\ alpha}\ alpha}\ alpha}\ mathrm {-}\ mathrm {-}\ tilde {\ delta} (\ frac {\ mathrm {\ partial}}\ overline {x}} {\ mathrm {\ partial}}\ overline {x}} {\ mathrm {\ partial}}\ overline {x}} {\ mathrm m {\ partial} {\ zeta} _ {\ alpha}})\ delta {\ alpha}})\ delta {\ alpha} ^ {\ zeta} ^ {\ zeta}\ overline {x}} {\ mathrm {\ alpha}} {\ mathrm {\ alpha}})\ delta {\ zeta}} {\ partial}})\ delta {\ zeta}} {\ zeta}} {\ partial}} {\ alpha}}\ tilde {\ delta}\ delta {\ zeta}}\ delta {\ zeta}} ^ {\ alpha})\]

The first variation of the term on the left of () is equal to:

\[\]

: label: eq-91

tilde {delta} ({d} _ {n} n)mathrm {=}tilde {delta} {d} _ {n} n+ {d} _ {d} _ {n} _ {n}n}tilde {delta} n

We will now calculate the second variation by applying the \(\tilde{\Delta }\) operator on (). It is written:

\[\]

: label: eq-92

tilde {Delta}tilde {delta} ({d} _ {n} n)mathrm {=}tilde {Delta}tilde {delta} {d} {d} _ {n} n+tilde {delta} n+tilde {delta} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {d} n+tilde {delta} {delta} n+ {d} _ {n}tilde {Delta}tilde {delta} n

By equating the two equations () and (), we get:

(2.75)\[\begin{split} \ begin {array} {c} ({\ Delta} _ {\ Delta} _ {t} {\ delta} _ {\ delta} _ {\ delta} _ {t}\ overline {x}\ overline {x}\ mathrm {-}\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {\ partial}} ({\ delta} _ {t}\ overline {x})} {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {\ partial}} ({\ delta} _ {t}\ overline {x})} {\ mathrm {x})} {\ mathrm {-} m {\ partial} {\ zeta} _ {\ alpha}}}\ Delta {\ zeta}}\ Delta {\ zeta}} ^ {\ zeta} ^ {x}} {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ zeta}} {\ partial}} {\ zeta}})\ delta {\ zeta}} (\ frac {\ mathrm {\ zeta}} {\ zeta}} (\ frac {\ mathrm {\ partial}}\ overline {x}}} {\ partial}} {\ alpha}})\ delta {\ zeta}} (\ frac {\ mathrm {\ partial}}\ overline {x}}} {\ alpha}} {\ partial}}\ mathrm {-}\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ tilde {\ Delta}\ delta {\ delta}\\ delta}\\ delta {\ delta}\\\ delta}\\ delta}\ delta}\ delta}\ delta}\ delta {\ delta}\ delta}\ delta {\ zeta}\ delta}\ delta {\ zeta}} ^ {\ zeta} ^ {\ zeta} ^ {\ alpha} ^ {\ alpha} ^ {\ alpha}) ^ {\ alpha})\ mathrm {\ alpha})\ mathrm {=}\ (\ tilde {\ delta} {\ delta} {d} _ {n} n+\ tilde {\ delta} {d} {d} _ {n}\ tilde {\ Delta} n+\ tilde {\ delta} {\ Delta} {d} _ {n}\ tilde {\ delta} n+ {d} _ {n}\ tilde {\ Delta}\ tilde {\ delta} n)\ end {delta} n)\ end {array}\end{split}\]

We’re going to multiply () by normal \(n\). We consider the properties () and (), that is to say:

(2.76)\[ \ frac {\ mathrm {\ partial}\ overline {x}}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}}\ mathrm {\ cdot}} n\ mathrm {\ cdot} n\ mathrm {=} 0\]

This gives us, after simplifications:

(2.77)\[ ({\ Delta} _ {t} {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {t}\ overline {x}\ mathrm {-}\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-} x\ mathrm {-} -}\ frac {\ mathrm {-} -}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {-}\ frac {\ mathrm {\ partial} {\ partial}} eta} _ {\ alpha}}\ Delta {\ zeta}} ^ {\ zeta} ^ {\ zeta}} ^ {\ zeta}}\ overline {x}} {\ mathrm {\ zeta}} {\ mathrm {\ partial}} {\ partial} {\ alpha}}\ mathrm {\ partial}} {\ alpha}} {\ alpha})\ mathrm {\ partial}} {\ alpha}} {\ mathrm {\ partial}} {\ partial}} {\ mathrm {\ partial}} {\ partial}} {\ alpha}} {\ mathrm {\ partial}} {\ partial}} {\ alpha}} {\ mathrm {\ partial}} {\ partial}} {\ alpha}} {\ mathrm {\ partial}} dot} n\ mathrm {=}\ tilde {\ Delta}\ tilde {\ Delta}\ tilde {\ delta} {\ delta} {d} _ {n}\ tilde {\ Delta} n)\ mathrm {\ Delta} n)\ mathrm {\ delta} n)\ mathrm {\ delta} n)\ mathrm {\ cdot} n\]

We know that \({d}_{n}\) is a purely Lagrangian quantity (§ 2.3.2), so:

(2.78)\[ \ tilde {\ delta} {d} _ {n}\ mathrm {=} {\ delta} _ {t} {d} _ {n}\]

It is assumed that the variations \({\Delta }_{t}{\delta }_{t}x\) and \({\Delta }_{t}{\delta }_{t}\overline{x}\) are zero. In addition, by analogy with (), we have:

(2.79)\[ \ tilde {\ Delta} n\ mathrm {\ cdot} n\ mathrm {=} 0\]

This gives us:

(2.80)\[ {\ Delta} _ {t} {\ delta} _ {t} {t} {d} _ {d} _ {n}\ mathrm {=} (\ mathrm {-}\ frac {\ mathrm {\ partial} ({\ delta}} _ {\ delta} _ {\ delta} _ {\ partial}} ({\ delta} _ {\ partial}} ({\ delta} _ {\ partial}} ({\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ delta} _ {\ zeta} _ {\ zeta}} ({\ delta} _ {\ zeta} _ {\ zeta}} ({\ delta} _ {\ zeta} _ {\ zeta}} ({\ delta} _ {\ delta} _ {\ delta} _ {\ alpha}\ mathrm {-}\ tilde {\ Delta} (\ tilde {\ Delta} (\ frac {\ mathrm {\ partial}} {\ partial} {\ zeta} _ {\ alpha}} _ {\ alpha}})\ delta {\ alpha}})\ delta {\ zeta}} ({\ alpha}})\ delta {\ zeta}} ({\ alpha}})\ delta {\ zeta}}})\ delta {\ zeta}} {\ alpha}})\ delta {\ zeta}}})\ delta {\ zeta}} {\ alpha}})\ delta {\ zeta}}})\ delta {\ zeta}} {\ alpha}})\ delta {\ zeta}}}\ delta {\ zeta}}} {n}\ tilde {\ Delta}\ tilde {\ delta} n)\ mathrm {\ cdot} n\]

We use ():

(2.81)\[ \ tilde {\ Delta} (\ frac {\ mathrm {\ partial}\ overline {x}} {\ mathrm {\ partial} {\ zeta} _ {\ alpha}})\ mathrm {=}\ frac {\ mathrm {\ partial}\ frac {\ partial}\ frac {\ mathrm {\ partial}} ({\ mathrm {\ partial}} ({\ partial})} {\ mathrm {\ partial} {\ partial} ({\ partial})} {\ mathrm {\ partial} {\ partial} ({\ partial})} {\ mathrm {\ partial} {\ partial} ({\ partial})} {\ mathrm {\ partial} {zeta} _ {\ alpha}} +\ frac {{\ mathrm {\ mathrm {\ partial}}} ^ {2}\ overline {x}} {\ partial} {\ zeta} {\ zeta} _ {\ alpha}\ mathrm {\ alpha}\ mathrm {\ alpha}\ mathrm {\ alpha}\ mathrm {\ alpha}\ mathrm {\ partial}\ mathrm {\ partial}} {\ beta}}\ Delta {\ zeta} ^ {\ beta} _ {\ beta}}\ Delta {\ zeta} ^ {\ beta}}\]

So:

\[\]

: label: eq-100

{Delta} _ {t} {delta} _ {t} {t} {d} _ {d} _ {n}mathrm {=} (mathrm {-}frac {mathrm {partial} ({delta}} _ {delta} _ {delta} _ {partial}} ({delta} _ {partial}} ({delta} _ {partial}} ({delta} _ {delta} _ {delta} _ {delta} _ {delta} _ {zeta} _ {zeta}} ({delta} _ {zeta} _ {zeta}} ({delta} _ {zeta} _ {zeta}} ({delta} _ {delta} _ {delta} _ {alpha}mathrm {-}delta {zeta}} ^ {zeta} ^ {zeta} ^ {partial}} ^ {2}overline {x}} {mathrm {partial} {partial} {zeta} {zeta} _ {alpha}mathrm {partial}} {zeta}} {beta}} {beta}} {beta}} {partial}} {partial}} {zeta}} {partial}} {zeta}} {beta}mathrm {-}frac {mathrm {partial} ({delta} _ {t}overline {x})} {mathrm {partial} {zeta} {zeta} _ {zeta} _ {alpha}} _ {alpha}}delta {alpha}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}}delta {zeta}}} n}tilde {Delta}tilde {delta} n)mathrm {cdot} n

We recognize the curvature tensor ():

\[\]

: label: eq-101

begin {array} {cc} {Delta} _ {Delta} _ {t} {delta} _ {t} {delta} _ {n}mathrm {-} nmathrm {cdot} (Delta {cdot}} (Delta {zeta}} (Delta {zeta}} (delta}}cdot} (Delta {cdot}) (Delta {zeta}} (Delta {zeta}} _ {zeta}} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta})} {mathrm {partial} {zeta} {zeta} _ {alpha}} +frac {mathrm {partial} ({delta} _ {t}overline {x})} {mathrm {partial})} {zeta} _ {alpha}}\ &mathrm {-}delta {zeta} _ {alpha} {alpha} {kappa} _ {alphabeta} _ {beta}\ &mathrm {-} ({d} _ {n}n}tilde {delta}}tilde {Delta}tilde {delta} nend {array} nend {array}

The expression for \(\tilde{\Delta }\tilde{\delta }n\mathrm{\cdot }n\) remains to be specified. We have:

\[\]

: label: eq-102

tilde {delta} nmathrm {cdot} nmathrm {=} 0totilde {Delta} (tilde {delta} nmathrm {cdot} n)mathrm {cdot} n)mathrm {=} 0totilde {delta}tilde {delta} nmathrm {cdot} nmathrm {=} 0totilde {delta} nmathrm {cdot} nmathrm {=}mathrm {-}tilde {delta} nmathrm {cdot}tilde {Delta} n

The Weingarten formula () gives us:

\[\]

: label: eq-103

tilde {Delta}tilde {delta} nmathrm {cdot} nmathrm {=}mathrm {-} (tilde {delta} (frac {mathrm {delta}} nmathrm {partial}}overline {cdot}} nmathrm {cdot}} nmathrm {cdot}} nmathrm {cdot}} nmathrm {cdot}} nmathrm {cdot}} nmathrm {cdot} nmathrm {cdot} nmathrm {cdot} nmathrm {cdot} nmathrm {cdot} nmathrm {dot} n)mathrm {cdot}frac {mathrm {partial}overline {x}} {mathrm {partial} {zeta} ^ {alpha}}mathrm {alpha}}}mathrm {cdot}} (mathrm {cdot} (tilde {partial}} (tilde {delta}} (tilde {delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (tilde {Delta}} (partial} {zeta} _ {beta}}})mathrm {cdot} n)mathrm {cdot}frac {mathrm {partial}overline {x}}overline {x}}} {mathrm {partial}} {partial} {beta}}

Since the dot product is commutative, using the contravariant metric tensor, we obtain:

\[\]

: label: eq-104

tilde {Delta}tilde {delta} nmathrm {cdot} nmathrm {=}mathrm {-} {m} ^ {alphabeta} (tilde {delta} (tilde {delta}} (tilde {delta}} (tilde {delta}} (tilde {delta}} (tilde {delta}} (tilde {delta}) (tilde {delta}} (tilde {delta}} (tilde {delta}} (tilde {delta}) (tilde {delta}} (tilde {delta}} (tilde {delta}} (tilde {delta}) (tilde {delta}}})mathrm {cdot} n) (tilde {Delta}} (frac {mathrm {partial}overline {x}} {mathrm {partial} {partial} {partial} {partial} {partial}} {partial}} {partial}} {partial}} {partial}} {partial}} {partial}} {partial}} {partial} {partial} {partial} {partial} {partial} {partial} {partial} {partial} {partial} {partial} {partial} {

Variations must be developed by applying expressions from ():

\[\]

: label: eq-105

tilde {Delta}tilde {delta} nmathrm {cdot} nmathrm {=}mathrm {-} {m} ^ {alphabeta} nmathrm {cdot} nmathrm {cdot} (frac {mathrm {cdot}} (frac {mathrm {partial}}) {mathrm {partial} ({delta} _ {t}overline {x})} {mathrm {x})} {mathrm {cdot} (frac {mathrm {partial}} ({delta}} {t}overline {x})} {mathrm {x})} {mathrmpartial} {zeta} _ {alpha}}} +frac {{mathrm {partial}} ^ {2}overline {x}} {mathrm {partial} {zeta} {zeta} _ {zeta} _ {alpha}} _ {partial}}delta {zeta}} ^ {zeta}} {zeta} _ {zeta}}delta {zeta} ^ {zeta} _ {zeta}) (frac {mathrm {partial} ({delta} _ {t}overline {x})} {mathrm {partial} {zeta} _ {beta}} +frac {{mathrm {mathrm {partial}}} ^ {partial}} ^ {2}overline {x}} {mathrm {partial}} {zeta}} _ {beta} _ {beta}mathrm _ {beta}mathrm {partial} {zeta} _ {sigma}}delta {zeta} ^ {sigma}) mathrm {cdot} n

Once again, we find the curvature tensor:

(2.82)\[\begin{split} \ tilde {\ Delta}\ tilde {\ delta} n\ mathrm {\ cdot} n\ mathrm {=}\ mathrm {-} {m} ^ {\ alpha\ beta} (n\ mathrm {\ delta}} (n\ mathrm {\ cdot}}\ cdot}\ frac {\ mathrm {\ cdot}}\ frac {\ mathrm {\ partial}} ({\ delta} _ {t}\ overline {x})} {\ mathrm {x})} {\ mathrm {\ cdot}\ frac {\ mathrm {\ partial} ({\ delta}} _ {t}\ overline {x})} {\ mathrm {x})} {\ mathrm {\ dot}}\\ partial} {\ zeta} _ {\ alpha}}} + {\ kappa}} + {\ kappa} _ {\ alpha\ gamma}\ delta {\ zeta} ^ {\ gamma}) (n\ mathrm {\ cdot}\ frac {\ alpha}}}\ frac {\ mathrm {\ alpha}}} {\ mathrm {\ cdot}\ frac {\ mathrm {\ alpha}}} {\ mathrm {\ cdot}\ frac {\ mathrm {\ alpha}}} {\ mathrm {\ cdot}\ frac {\ mathrm {\ alpha}}} {\ mathrm {\ zeta}} _ {\ beta}} + {\ kappa} _ {\ beta\ sigma}\ delta {\ zeta} ^ {\ sigma})\end{split}\]

Finally:

\[\]

: label: eq-107

begin {array} {cc} {Delta} _ {Delta} _ {t} {delta} _ {t} {delta} _ {n}mathrm {-} nmathrm {cdot} (Delta {cdot}} (Delta {zeta}} (Delta {zeta}} (delta}}cdot} (Delta {cdot}) (Delta {zeta}} (Delta {zeta}} _ {zeta}} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta} _ {zeta})} {mathrm {partial} {zeta} {zeta} _ {alpha}} +frac {mathrm {partial} ({delta} _ {t}overline {x})} {mathrm {partial})} {zeta} _ {alpha}}\ &mathrm {-}delta {zeta} _ {alpha} {alpha} {kappa} _ {alphabeta} _ {zeta} _ {beta}\ &mathrm {-} {d} _ {n} {d} _ {n} {m}}} {m}} ^ {m}} ^ {alphabeta} ^ {alphabeta} (nmathrm {cdot}}frac {mathrm {partial} ({delta}) _ {t}overline {x})} {mathrm {partial} {partial} {zeta} _ {alpha}} + {kappa} _ { alphagamma}delta {zeta} ^ {gamma} ^ {gamma}) (nmathrm {cdot}frac {mathrm {partial} ({delta} _ {t}overline {x})} {overline {x})}} {mathrm {partial})}} {mathrm {partial} {gamma})} {mathrm {partial} {zeta}} _ {betasigma}overline {x})}} {mathrm {partial} {partial}}} {mathrm {partial} {zeta}} _ {betasigma}overline {x})}} {mathrm {partial} {partial}} zeta} ^ {sigma})end {array})

[1]

The metric tensor is often referred to as an « index elevator »