1. Reference problem#
1.1. Geometry#
Consider a reinforced concrete cube with side \(L\mathrm{=}1m\).
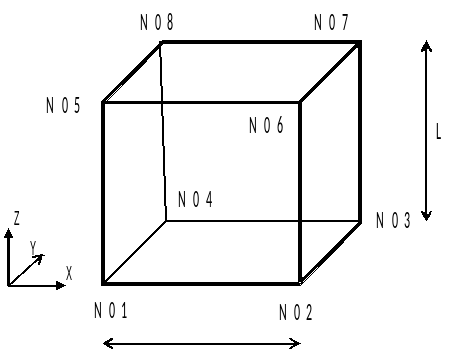
The reinforcement sheets belong to the plane defined by the four \(\mathit{N05}\mathrm{-}\mathit{N02}\mathrm{-}\mathit{N03}\mathrm{-}\mathit{N08}\) nodes.
Two reinforcement layers are defined: one in the local direction \(X\) and one in the local direction \(Y\).
The reinforcement rate for each reinforcing sheet is \(0.1{m}^{2}\mathrm{/}\mathit{ml}\) (Section per linear meter).
1.2. Characteristics of the models#
The concrete mesh is modelled with a hexa8 element.
The models considered for reinforcing plies are:
modeling A (§3): use of grid_membranewith tria3 support meshes
modeling B (§4): use of grid_membrane with quad4 support meshes
C modeling (§5): use of grille_excenter with tria3 support meshes
1.3. Material properties#
The concrete material is isotropic elastic whose properties are:
\({E}_{b}=20000\mathrm{MPa}\)
\(\nu =0.2\)
The law of behavior of reinforcements follows an elastoplastic model whose properties are:
\({E}_{a}=200000\mathrm{MPa}\)
\(\nu =0\)
\({E}_{\mathrm{ecr}}^{\mathrm{acier}}=20000\mathrm{MPa}\)
\({\sigma }_{e}^{\mathrm{acier}}=200000\mathrm{MPa}\)
The grid_isot_line model for isotropic work hardening plasticity is used in stat_non_line.
1.4. Boundary conditions and loads#
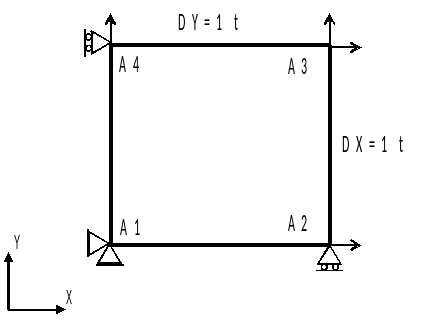
Boundary conditions:
Embedding in \(\mathit{A1}\)
\(\mathit{DX}\mathrm{=}0\) on the \(\mathit{A1}\mathrm{-}\mathit{A4}\) ridge
\(\mathit{DY}\mathrm{=}0\) on the \(\mathit{A1}\mathrm{-}\mathit{A2}\) ridge
\(\mathrm{DZ}=0\) on the bottom surface of the cube (N01-N02-N03-N04)
Charging by mandatory trips:
\(\mathrm{DX}=1\) on the \(\mathit{A2}\mathrm{-}\mathit{A3}\) ridge
\(\mathit{DY}\mathrm{=}1t\) on the \(\mathit{A3}\mathrm{-}\mathit{A4}\) ridge
where \(t\) is the pseudotime parameter.
1.5. Initial conditions#
Initially, travel and constraints were zero everywhere.