7. E modeling#
7.1. Characteristics of modeling E#
Modeling AXIS.
Model of DRUCK_PRAG_N_A with linear, parabolic and exponential negative work hardening.
Number of nodes |
\(4\) |
|||
Number of meshes |
\(5\) |
That is: |
||
SEG2 |
|
|||
QUAD4 |
|
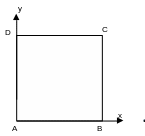
The square is in space \([0.\mathrm{,1}\mathrm{.}]\text{x}[0.\mathrm{,1}\mathrm{.}]\).
Coordinates of points \((m)\):
\(A:(0.,0.)\)
\(B:(1.,0.)\)
\(C:(1.,1.)\)
\(D:(0.,1.)\)
Knitwear:
\(\mathrm{M1}\): surface \(\mathrm{ABDC}\)
\(\mathrm{M2}\): segment \(\mathrm{AB}\)
\(\mathrm{M3}\): segment \(\mathrm{BC}\)
\(\mathrm{M4}\): segment \(\mathrm{CD}\)
\(\mathrm{M5}\): segment \(\mathrm{DA}\)
Node groups:
\(A,B\)
7.2. Tested sizes and results#
Grandeur |
Point |
NUME_ORDRE |
Reference, linear work hardening |
Reference, parabolic work hardening |
Reference, exponential work hardening |
Tolerance \(\text{\%}\) |
\(\mathit{SIZZ}(N/{m}^{2})\) |
A |
9 |
\(-8.77\mathrm{.}{10}^{6}\) |
\(-8.76\mathrm{.}{10}^{6}\) |
\(-8.77\mathrm{.}{10}^{6}\) |
0.1 |
34 |
\(-7.20\mathrm{.}{10}^{6}\) |
\(-6.44\mathrm{.}{10}^{6}\) |
\(-7.55\mathrm{.}{10}^{6}\) |
0.1 |
||
60 |
\(-5.86\mathrm{.}{10}^{6}\) |
\(-5.80\mathrm{.}{10}^{6}\) |
/ |
0.1 |
||
\(\mathrm{V1}\) |
A |
9 |
\(4.69\mathrm{.}{10}^{-5}\) |
\(5.11\mathrm{.}{10}^{-5}\) |
\(4.69\mathrm{.}{10}^{-5}\) |
0.1 |
34 |
\(5.3\mathrm{.}{10}^{-3}\) |
\(5.4\mathrm{.}{10}^{-3}\) |
\(5.3\mathrm{.}{10}^{-3}\) |
0.1 |
||
60 |
\(9.8\mathrm{.}{10}^{-3}\) |
\(9.8\mathrm{.}{10}^{-3}\) |
/ |
0.1 |
||
\(\mathrm{DY}(m)\) |
A |
9 |
\(-1.2\mathrm{.}{10}^{-3}\) |
\(-1.2\mathrm{.}{10}^{-3}\) |
\(-1.2\mathrm{.}{10}^{-3}\) |
0.1 |
34 |
\(-4.9\mathrm{.}{10}^{-3}\) |
\(-4.9\mathrm{.}{10}^{-3}\) |
\(-4.9\mathrm{.}{10}^{-3}\) |
0.1 |
||
60 |
\(-8.8\mathrm{.}{10}^{-3}\) |
\(-8.8\mathrm{.}{10}^{-3}\) |
/ |
0.1 |