1. Reference problem

1.1. Geometry

We consider a square plate with side \(20m\) in plane deformations, centered in the \((X,Y)\) coordinate system. The cracks are defined by the points \(A\) to \(J\) and \(A\text{'}\) to \(J\text{'}\), whose coordinates are given in table 1. The cracks are shown in FIG. 1.

Points	\(X\)	\(Y\)		Points	\(X\)	\(Y\)
\(A\)	−3.0851	0.75		\(A\text{'}\)	3,08512	−0.75
\(B\)	0.50000	1,13327		\(B\text{'}\)	−0.5000	−0.3667
\(C\)	0.20309	1,55730		\(C\text{'}\)	−0.2031	0.05730
\(D\)	−2,1454	1.09202		\(D\text{'}\)	2,14543	−0.4080
\(E\)	−1.3794	0.44923		\(E\text{'}\)	1,37939	−1.0508
\(F\)	−3.0851	−0.25		\(F\text{'}\)	3,08512	−1.75
\(G\)	−2.3780	0.45711		\(G\text{'}\)	2,37802	−1.0429
\(H\)	−1.3794	1.09202		\(H\text{'}\)	1,37939	−0.4080
\(I\)	−0.5134	1,59202		\(I\text{'}\)	0.51336	0.09202
\(J\)	−0.4397	0.79125		\(J\text{'}\)	0.43969	−0.7087

Table 1: coordinates of the points defining the cracks.

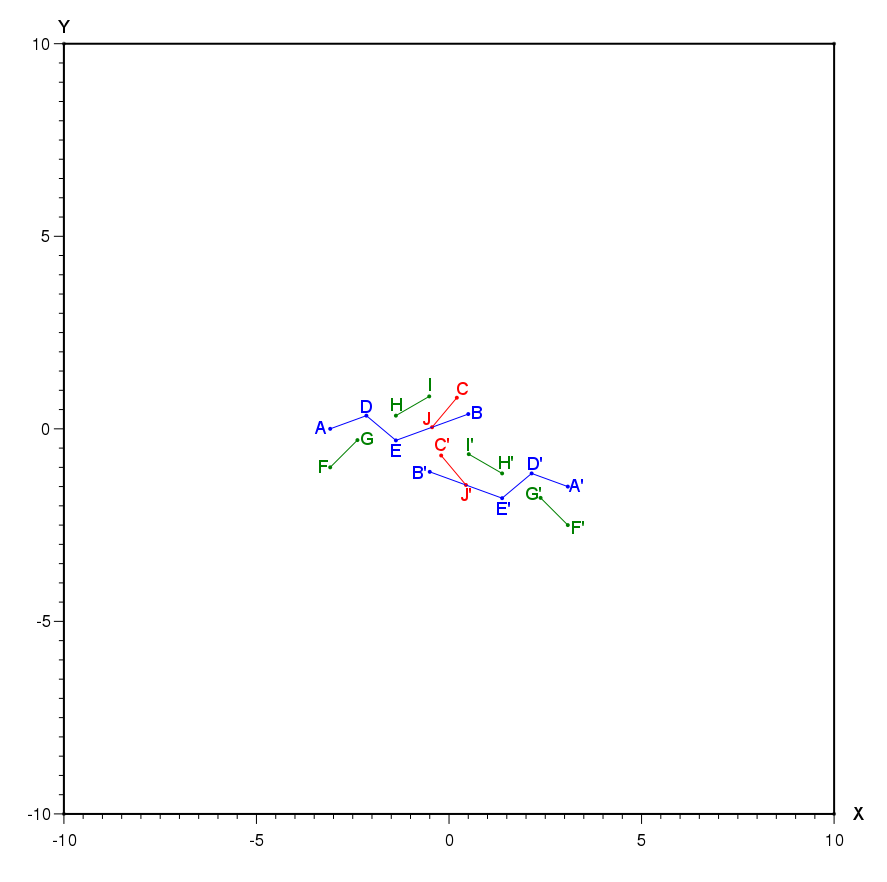
Figure 1: position of points and cracks.

1.2. Material properties

The material is isotropic elastic with the following properties:

• \(E\mathrm{=}\mathrm{0,1}\mathit{MPa}\)

• \(\nu =0.3\)

1.3. Boundary conditions and loads

Constraint \(\sigma \mathrm{=}(\begin{array}{cc}1& 1\\ 1& 1\end{array})\) is imposed on the entire outline of the structure. This corresponds to a loading in bi-traction and unit shear. Rigid fashions are blocked.

Figure 2: loading the structure.