3. Modeling A

3.1. Characteristics of modeling

We use a D_ PLAN modeling. The cracks are introduced with X- FEM using the GROUP_MA_FISS and GROUP_MA_FOND operands of the DEFI_FISS_XFEM operator. In fact, the points given in table 1 make it possible to easily generate mesh lines representing the cracks in FIG. 1. The possible contact between the crack lips is not taken into account in order to respect the hypothesis of free stresses on the crack lips of the reference solution.

3.2. Characteristics of the mesh

The initial adjusted mesh composed of 400 cells of type QUAD4 in FIG. 3 is refined adaptively in 3 iterations using commands RAFF_XFEM and MACR_ADAP_MAIL. The final refined mesh around the crack bottoms in FIG. 4 is obtained, composed of 17105 cells of type QUAD4 and 2076 cells of type TRIA3.

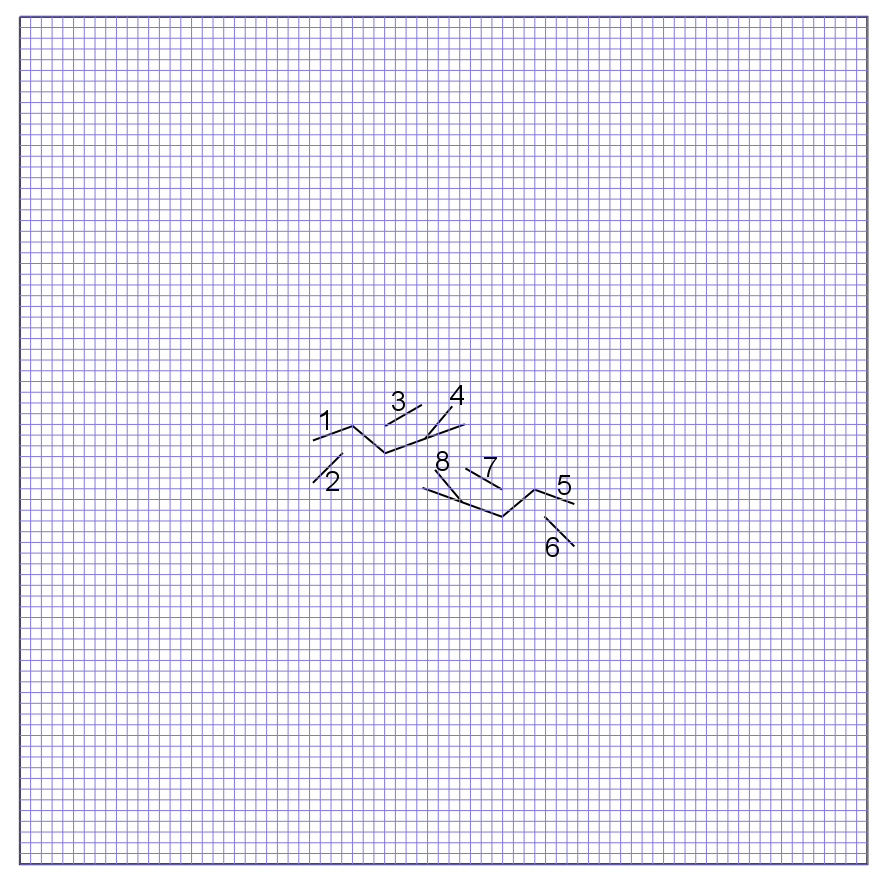
Figure 3: initial mesh size and crack numbering.

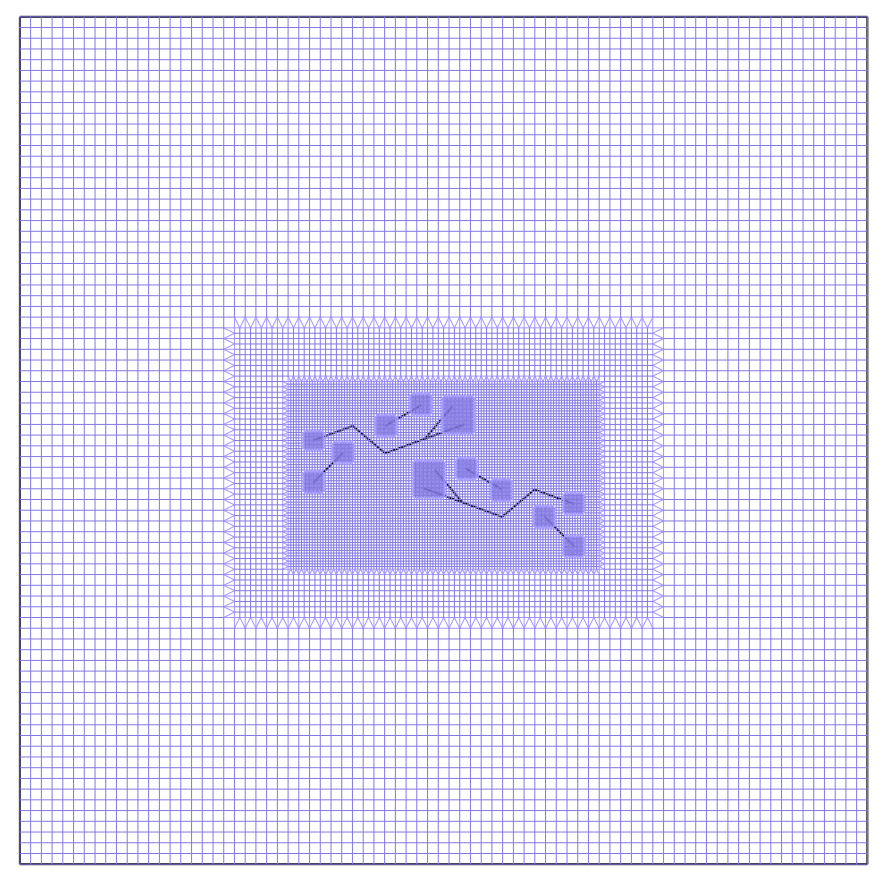
Figure 4: refined mesh around the crack bottoms used for the calculation.

3.3. Tested sizes and results

The stress intensity factors on the points of the crack bottoms are tested with respect to the values given in Table 2. Stress intensity factors are calculated using option CALC_K_G of the CALC_G operator.

The values are validated with a tolerance of 1%. However, it should be noted that it is numerically possible to converge on the semi-analytical solution by refining the mesh.

Identification	Reference type	Reference value	Tolerance
Point \(A\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(A\) - \({K}_{2}\)	“ANALYTIQUE”	2.8522	1.1%
Point \(B\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(B\) - \({K}_{2}\)	“ANALYTIQUE”	2.4042	1.1%
Point \(C\) - \({K}_{1}\)	“ANALYTIQUE”	-1.6920	1.1%
Point \(C\) - \({K}_{2}\)	“ANALYTIQUE”	-0.1337	1.1%
Point \(F\) - \({K}_{1}\)	“ANALYTIQUE”	0.0510	1.1%
Point \(F\) - \({K}_{2}\)	“ANALYTIQUE”	0.2894	1.1%
Point \(G\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(G\) - \({K}_{2}\)	“ANALYTIQUE”	0.1885	1.1%
Point \(H\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(H\) - \({K}_{2}\)	“ANALYTIQUE”	-0.1979	1.1%
Point \(I\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(I\) - \({K}_{2}\)	“ANALYTIQUE”	0.0213	1.1%
Point \(A\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	0.0000	1.1%
Point \(A\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	2.3379	1.1%
Point \(B\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	2.6700	1.1%
Point \(B\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	1.0248	1.1%
Point \(C\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	5.3966	1.1%
Point \(C\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	-0.1143	1.1%
Point \(F\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	4.3255	1.1%
Point \(F\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	-0.1661	1.1%
Point \(G\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	3.6812	1.1%
Point \(G\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	0.9279	1.1%
Point \(H\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	0.4157	1.1%
Point \(H\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	-0.3947	1.1%
Point \(I\text{'}\) - \({K}_{1}\)	“ANALYTIQUE”	1.0043	1.1%
Point \(I\text{'}\) - \({K}_{2}\)	“ANALYTIQUE”	0.0648	1.1%