1. Reference problem#

1.1. Geometry#

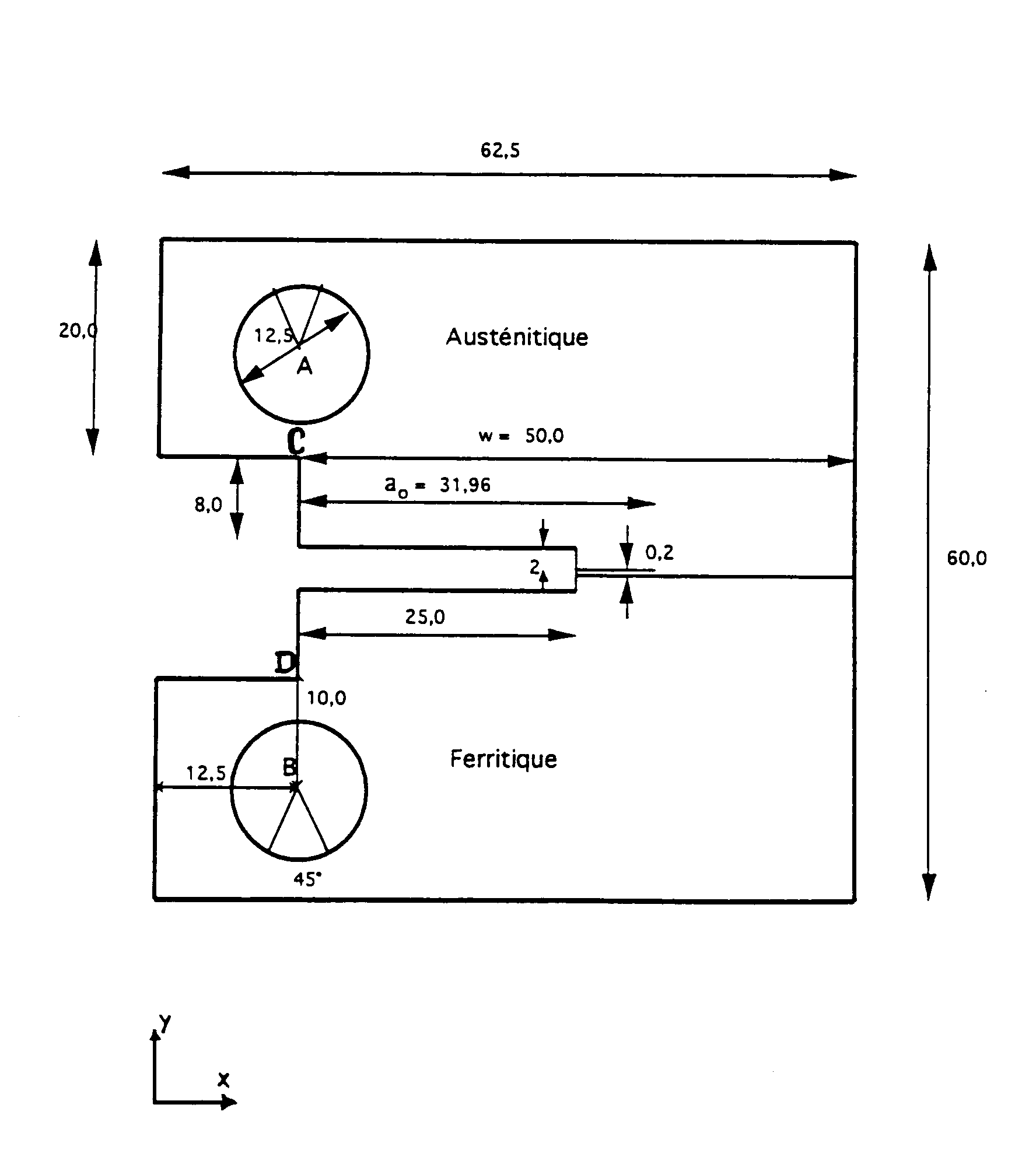
All ratings are in \(\mathrm{mm}\). The crack is located \(\mathrm{0,2}\mathrm{mm}\) from the interface, in the upper part of the specimen.

Material #1: austenitic steel

Von Mises elastoplastic with isotropic work hardening

Young’s modulus \({E}_{1}\mathrm{=}{2.10}^{5}\mathit{MPa}\), Poisson’s ratio \({\nu }_{1}=\mathrm{0,3}\)

Elastic limit \({\sigma }_{\mathit{y1}}\mathrm{=}310\mathit{MPa}\)

Uniaxial tensile curve:

\(\sigma (\mathrm{MPa})\)	0	310	310	600	700
\(\varepsilon\)	0	0.155	0.155	40	100

Material #2: ferritic steel

Von Mises elastoplastic with isotropic work hardening

Young’s modulus \({E}_{2}={2.10}^{5}\mathrm{MPa}\), Poisson’s ratio \({\nu }_{2}=\mathrm{0,3}\)

Elastic limit \({\sigma }_{\mathrm{y2}}=442\mathrm{MPa}\)

\(\sigma (\mathrm{MPa})\)	0	442	442	600	650
\(\varepsilon\)	0	0.221	40	100

Material #3: almost non-deformable pins

Isotropic linear elastic

Young’s modulus \({E}_{3}={6.10}^{10}\mathrm{MPa}\), Poisson’s ratio \({\nu }_{3}=\mathrm{0,3}\)

Given the asymmetry of the materials, the entire specimen is modelled.

Blocks:

\(\mathrm{UX}=\mathrm{UY}=0\)	at point \(B\) (center of the lower pin)
\(\mathrm{UX}=0\)	at point \(A\) (center of the top pin)

Loading per imposed displacement:

\[\]

: label: EQ-None

0lemathrm {UY}le 1mathrm {mm}

The load is therefore monotonous and increasing.