2. Benchmark solution#

2.1. Calculation method used for the reference solution#

The reference solution used is a semi-empirical formula based on the work of ASTM [bib1].

2.2. Benchmark results#

The formula for ASTM for the Rice integral \(J\) is as follows:

\({J}_{\mathit{ASTM}}\mathrm{=}(2+\mathrm{0,522}\mathrm{\ast }{b}_{0}\mathrm{/}w)\mathrm{\ast }A\mathrm{/}{b}_{0}\),

where \({b}_{0}=w-{a}_{0}\) is the initial length of the ligament and \(A\) is the area under the load—displacement curve at point \(A\), i.e. the work of the load applied.

The integral \({J}_{\mathit{ASTM}}\) is compared in the figure below to the energy recovery rate \(G\) resulting from a finite element calculation with CASTEM2000 and the theta [bib2] method. The force-displacement response curve and the opening of the crack lips calculated by finite elements are also plotted.

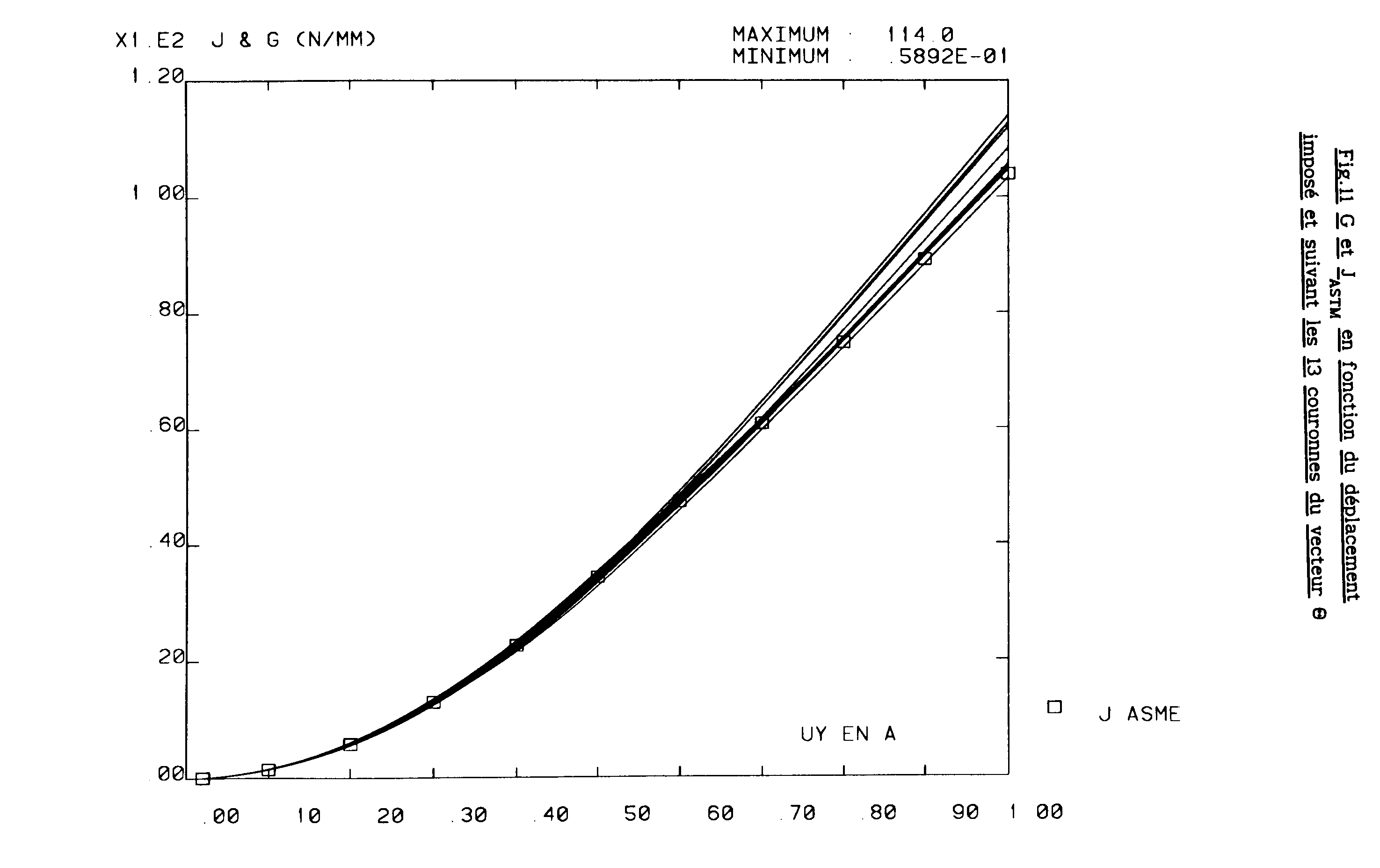
_images/1000000000000B8600000740F30BBBACA04E8F5D.png

Energy return rate \(G\) depending on displacement in \(A\)

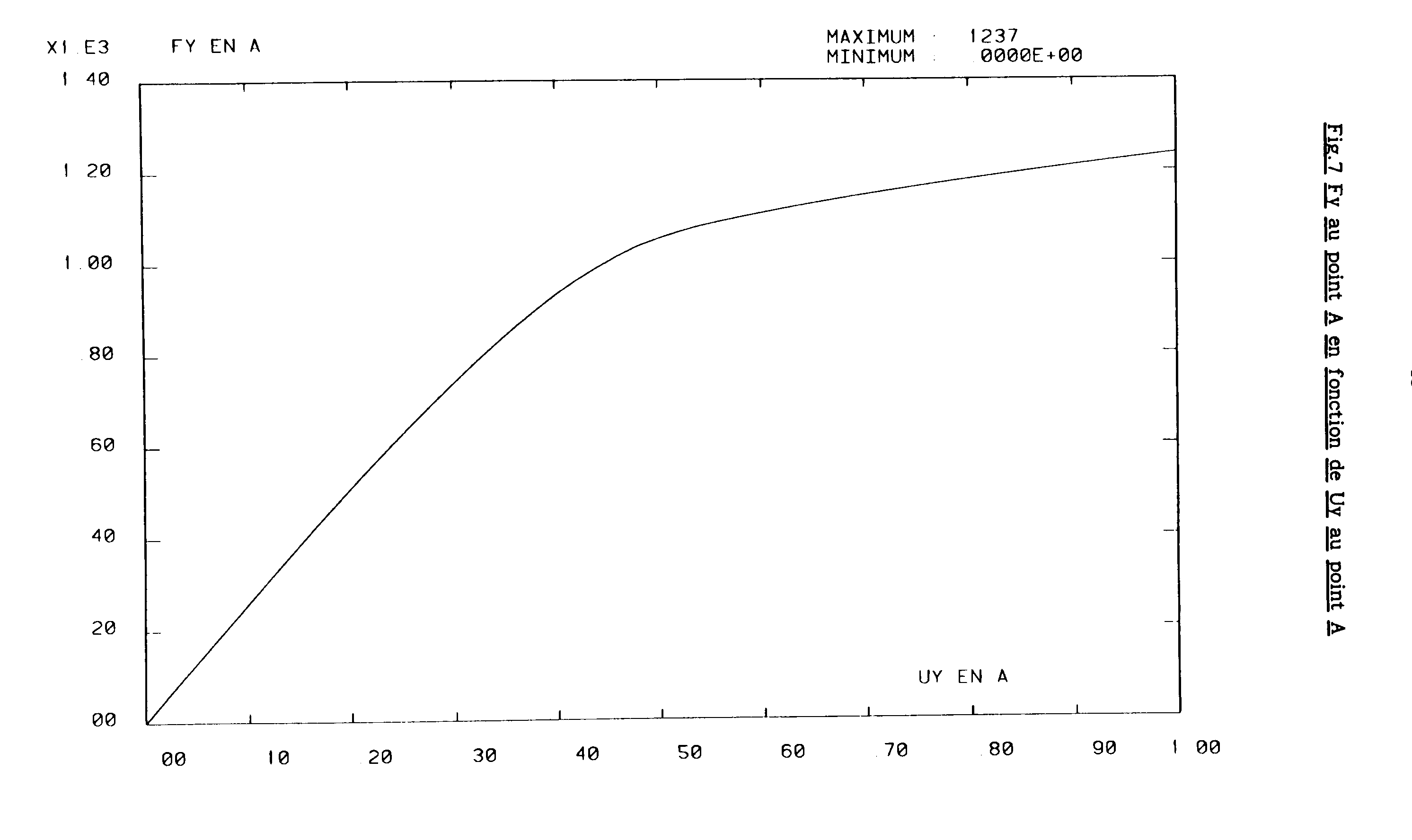
_images/1000000000000BA8000006F0FA44D4E5BDF9F987.png

Force-displacement response curve at point \(A\)

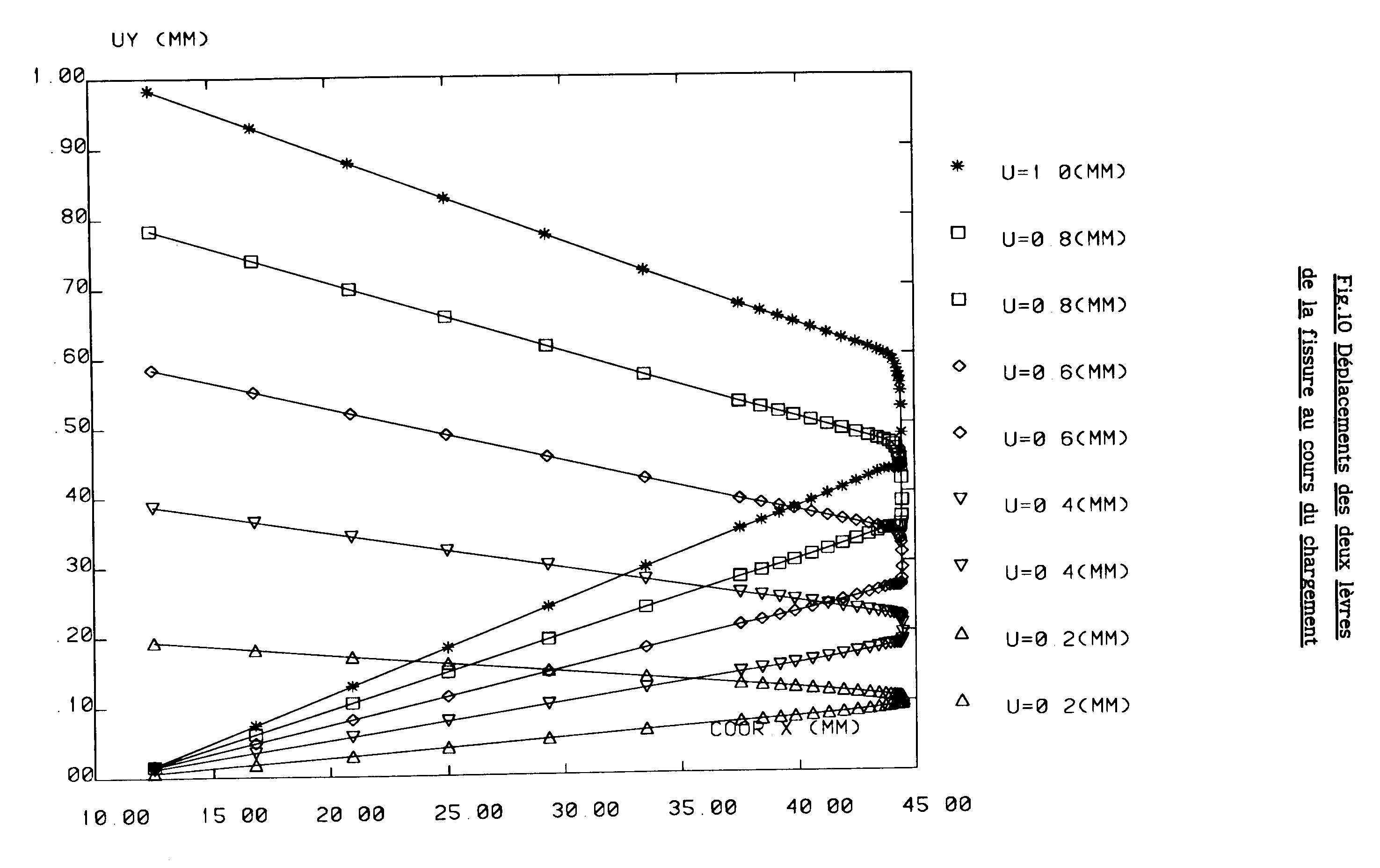
_images/1000000000000B860000074098C07397328D34EB.png

Vertical movement of the two crack lips

2.3. Uncertainty about the solution#

It should be noted that the reference solution is not an exact solution and that it does not apply, in general, in the case of bi-materials. However, it can be used for this study because the crack is not located at the interface of the two materials.

The maximum difference between the CASTEM2000 results and the ASTM formula is approximately \(\text{9 \%}\) for the first ring (closest to the crack) and the maximum load. This difference decreases when you take crowns farther away from the bottom of the crack.

The Castem 2000 calculation was carried out on the same mesh as the modeling A of this test case.

2.4. Bibliographical references#

  1. American Society for Testing and Materials. Annual Book of ASTM Standards, vol. 3.01, Section 3, Metals Test Methods and Analytical Procedures, article E813, page 711, 1990.

  2. X.Z. SUO and J. BROCHARD: Elasto-plastic calculation of a bimetallic CT specimen with a crack close to the interface. Report CEA DMT /94-132