1. Reference problem

1.1. Geometry

The structure is composed of two concentric circular crowns. The inner radius \({R}_{2}\) of the outer ring is equal to the outer radius of the inner ring (Figure 1.1-1).

The characteristic dimensions of the structure are:

\({R}_{1}\mathrm{=}\mathrm{1,0}m;{R}_{2}\mathrm{=}\mathrm{0,6}m;{R}_{3}\mathrm{=}\mathrm{0,2}m\)

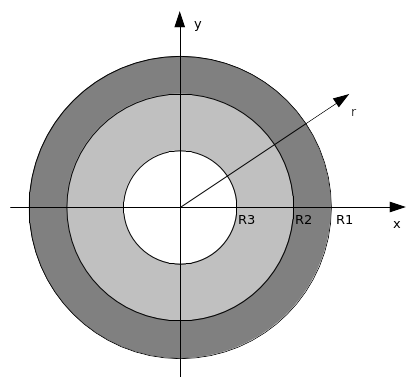
Figure 1.1-a : Structure geometry

1.2. Material properties

The Young’s modulus and the Poisson’s ratio of the material in the outer ring are given by \({E}_{1}\) and \({\nu }_{1}\) (respectively \({E}_{2}\) and \({\nu }_{2}\) for the inner ring).

1.3. Boundary conditions and loads

The application of a non-uniform pressure on the edge \(r={R}_{1}\) of the outer ring will be modelled as follows: \(p={\alpha }_{0}+{\alpha }_{1}\mathrm{.}\mathrm{cos}(2\theta )\), \(\theta\) being the polar angle describing the position of the point \(\theta =\mathrm{arctan}(\frac{Y}{X})\). For the analytical calculation, we will first solve the problem for a pressure \(p={\alpha }_{0}\), then we will try to solve the problem for a pressure of the form \(p={\alpha }_{1}\mathrm{.}\mathrm{cos}(2\theta )\). Then the principle of superposition will be applied.

1.3.1. Boundary conditions in the case of uniform pressure

The edges of the rings are subjected to displacements (\(r={R}_{1}\) and \(r={R}_{3}\)) equivalent to the application of pressure \(p={\alpha }_{0}\) on the edge of the outer ring (\(r={R}_{1}\)).

\(\begin{array}{c}{\xi }_{X}(r)=f(r)\mathrm{cos}(\mathrm{arctan}(\frac{Y}{X}))\\ {\xi }_{Y}(r)=f(r)\mathrm{sin}(\mathrm{arctan}(\frac{Y}{X}))\end{array}\)

The function \(f(r)\) of the radial displacement is given as a function of the properties of the materials and the pressure \(p\). It is of the form \({A}_{i}r+\frac{{B}_{i}}{r};i=\mathrm{1,2}\), in each field. In the case of plane deformations (MODELISATION = “D_ PLAN “) we have:

\(\begin{array}{c}f({R}_{1})={A}_{1}{R}_{1}+\frac{{B}_{1}}{{R}_{1}}\\ f({R}_{3})={A}_{2}{R}_{3}+\frac{{B}_{2}}{{R}_{3}}\end{array}\) eq 1.1

with:

\(\begin{array}{c}{A}_{1}=\frac{(1+{\nu }_{1})(1-2{\nu }_{1})}{{E}_{1}}\frac{-p{R}_{1}^{2}+\lambda {R}_{2}^{2}}{{R}_{1}^{2}-{R}_{2}^{2}};{B}_{1}=\frac{1+{\nu }_{1}}{{E}_{1}}(-p+\lambda )\frac{{R}_{1}^{2}{R}_{2}^{2}}{{R}_{1}^{2}-{R}_{2}^{2}}\\ {A}_{2}=\frac{-(1+{\nu }_{2})(1-2{\nu }_{2})}{{E}_{2}}\lambda \frac{{R}_{2}^{2}}{{R}_{2}^{2}-{R}_{3}^{2}};{B}_{2}=\frac{-1+{\nu }_{2}}{{E}_{2}}\lambda \frac{{R}_{2}^{2}{R}_{3}^{2}}{{R}_{2}^{2}-{R}_{3}^{2}}\end{array}\) eq 1.2

where \(\lambda\) is the contact pressure whose analytic expression is:

\(\lambda =2p(1-{\nu }_{1})\frac{\frac{{R}_{1}^{2}}{{R}_{1}^{2}-{R}_{2}^{2}}}{\frac{{R}_{1}^{2}+{R}_{2}^{2}(1-2{\nu }_{1})}{{R}_{1}^{2}-{R}_{2}^{2}}+\frac{{E}_{1}}{{E}_{2}}\frac{(1+{\nu }_{2})}{(1+{\nu }_{1})}\frac{{R}_{2}^{2}(1-2{\nu }_{2})+{R}_{3}^{2}}{{R}_{2}^{2}-{R}_{3}^{2}}}\) eq. 1.3

1.3.2. Boundary conditions in the case of variable pressure

The edges of the rings are subjected to displacements (\(r={R}_{1}\) and \(r={R}_{3}\)) equivalent to the application of pressure \(p={\alpha }_{1}\mathrm{.}\mathrm{cos}(2\theta )\) on the edge of the outer ring (\(r={R}_{1}\)).

\(\begin{array}{c}{\xi }_{X}(r,\theta )={u}_{r}(r,\theta )\mathrm{cos}(\theta )-{u}_{\theta }(r,\theta )\mathrm{sin}(\theta )\\ {\xi }_{Y}(r,\theta )={u}_{r}(r,\theta )\mathrm{sin}(\theta )+{u}_{\theta }(r,\theta )\mathrm{cos}(\theta )\end{array}\)

The function \({u}_{r}(r,\theta )\) of the radial displacement, and that of the tangential displacement \({u}_{\theta }(r,\theta )\), are given as a function of the properties of the materials, the pressure \(p\), the geometric characteristics and the square of the relationships between the radii: \({f}_{1}={(\frac{{R}_{2}}{{R}_{1}})}^{2};{f}_{2}={(\frac{{R}_{3}}{{R}_{2}})}^{2}\). In the case of plane deformations (MODELISATION = “D_ PLAN “) we have:

\(\begin{array}{c}{u}_{r}({R}_{\mathrm{1,}}\theta )=\frac{1+{\nu }_{1}}{{E}_{1}}[(-{\mathrm{2A}}_{1}{R}_{1}+2\frac{{C}_{1}}{{R}_{1}^{3}}+4\frac{{D}_{1}}{{R}_{1}})-{\nu }_{1}(4{B}_{1}{R}_{1}^{3}+4\frac{{D}_{1}}{{R}_{1}})]\mathrm{cos}(2\theta )\\ {u}_{\theta }({R}_{\mathrm{1,}}\theta )=\frac{1+{\nu }_{1}}{{E}_{1}}[({\mathrm{2A}}_{1}{R}_{1}+{\mathrm{6B}}_{1}{R}_{1}^{3}+2\frac{{C}_{1}}{{R}_{1}^{3}}-2\frac{{D}_{1}}{{R}_{1}})-{\nu }_{1}({\mathrm{4B}}_{1}{R}_{1}^{3}-4\frac{{D}_{1}}{{R}_{1}})]\mathrm{sin}(2\theta )\\ {u}_{r}({R}_{\mathrm{3,}}\theta )=\frac{1+{\nu }_{2}}{{E}_{2}}[(-{\mathrm{2A}}_{2}{R}_{3}+2\frac{{C}_{2}}{{R}_{3}^{3}}+4\frac{{D}_{2}}{{R}_{3}})-{\nu }_{2}(4{B}_{2}{R}_{3}^{3}+4\frac{{D}_{2}}{{R}_{3}})]\mathrm{cos}(2\theta )\\ {u}_{\theta }({R}_{\mathrm{3,}}\theta )=\frac{1+{\nu }_{2}}{{E}_{2}}[({\mathrm{2A}}_{2}{R}_{3}+{\mathrm{6B}}_{2}{R}_{3}^{3}+2\frac{{C}_{2}}{{R}_{3}^{3}}-2\frac{{D}_{2}}{{R}_{3}})-{\nu }_{2}({\mathrm{4B}}_{2}{R}_{3}^{3}-4\frac{{D}_{2}}{{R}_{3}})]\mathrm{sin}(2\theta )\end{array}\) eq 1.4

with:

\(\begin{array}{c}{A}_{1}=\frac{{\alpha }_{1}(2{f}_{1}^{2}+{f}_{1}+1)-\lambda ({f}_{1}^{3}+{f}_{1}^{2}+2{f}_{1})}{2{(1-{f}_{1})}^{3}};{B}_{1}=\frac{-1}{{R}_{2}^{2}}\frac{{\alpha }_{1}(3{f}_{1}^{2}+{f}_{1})-\lambda ({f}_{1}^{3}+3{f}_{1}^{2})}{6{(1-{f}_{1})}^{3}};\\ {C}_{1}={R}_{2}^{4}\frac{{\alpha }_{1}({f}_{1}+3)-\lambda ({\mathrm{3f}}_{1}+1)}{6{(1-{f}_{1})}^{3}};{D}_{1}=-{R}_{2}^{2}\frac{{\alpha }_{1}({f}_{1}^{2}+{f}_{1}+2)-\lambda (2{f}_{1}^{2}+{f}_{1}+1)}{2{(1-{f}_{1})}^{3}}\\ {A}_{2}=\frac{\lambda (2{f}_{2}^{2}+{f}_{2}+1)}{2{(1-{f}_{2})}^{3}};{B}_{2}=\frac{-1}{{R}_{3}^{2}}\frac{\lambda (3{f}_{2}^{2}+{f}_{2})}{6{(1-{f}_{2})}^{3}};\\ {C}_{2}={R}_{3}^{4}\frac{\lambda ({f}_{2}+3)}{6{(1-{f}_{2})}^{3}};{D}_{2}=-{R}_{3}^{2}\frac{\lambda ({f}_{2}^{2}+{f}_{2}+2)}{2{(1-{f}_{2})}^{3}}\end{array}\) eq 1.5

where \(\lambda\) is the contact pressure whose analytic expression is:

\(\lambda =\frac{{\mathit{coef}}_{1}}{{\mathit{coef}}_{2}+{\mathit{coef}}_{3}}{\alpha }_{1}\) eq 1.6

such as:

\(\begin{array}{c}{\mathit{coef}}_{1}=\frac{1+{\nu }_{1}}{6{E}_{1}{(1-{f}_{1})}^{3}}[(-12{f}_{1}^{2}-8{f}_{1}-12)-{\nu }_{1}(-12{f}_{1}^{2}-8{f}_{1}-12)]\\ {\mathit{coef}}_{2}=\frac{1+{\nu }_{1}}{6{E}_{1}{(1-{f}_{1})}^{3}}[(-3{f}_{1}^{3}-15{f}_{1}^{2}-9{f}_{1}-5)-{\nu }_{1}(-2{f}_{1}^{3}-18{f}_{1}^{2}-6{f}_{1}-6)]\\ {\mathit{coef}}_{3}=\frac{1+{\nu }_{2}}{6{E}_{2}{(1-{f}_{2})}^{3}}[(-5{f}_{2}^{3}-9{f}_{2}^{2}-15{f}_{2}-3)-{\nu }_{2}(-6{f}_{2}^{3}-6{f}_{2}^{2}-18{f}_{2}-2)]\end{array}\) eq 1.7