1. Reference problem#
The reference problem is based on the study presented in [bia1] _ and [bib2] _. The material of the tube is assumed to be elastoplastic with isotropic work hardening and the Von Mises criterion, described by a traction curve with a plastic plate. A complicated pressure loading path is chosen, showing phases such as expansion or contraction of the tube (slight pinching) and phases of the « rolling » type (strong pinching), in such a way as to enter the plastic field. We are also interested in the residual state.
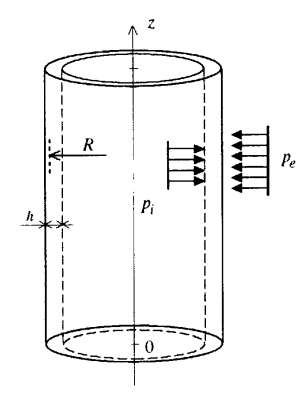
Fig. 1.1 Internal/external pressure pipe diagram#
- Two different axisymmetric pressure loading paths are envisaged:
path 1: alternating asynchronous internal/external pressures until complete discharge of the elastoplastic tube with isotropic work hardening. This path is inspired by the dudgeoning of tubes in a tube plate.
path 2: monotonic internal pressure increasing to the ruin limit, with control in radial displacement of the elastoplastic tube with isotropic work hardening. The progression of the plastic flow zone through the thickness is decisive in describing the occurrence of the ruin. In all cases, the first plasticization appears on the inner wall. This path is inspired by a burst pressure test for tubes.
1.1. Geometry#
Three geometries of tubes of varying thinness are treated:
Table 1-1: Tube dimensions.
Tube |
1 |
2 |
3 |
Medium radius \(R\) (\(\mathit{mm}\)) |
10 |
10 |
10 |
Thickness \(h\) (\(\mathit{mm}\)) |
0.5 |
1.0 |
2.0 |
1.2. Material and behavior#
- The material parameters are as follows:
Young’s modulus: \(E=\mathrm{187500}\mathit{MPa}\)
Poisson’s ratio: \(\nu=\mathrm{0.3}\)
elastic limit: \({\sigma}_{y}=\mathrm{330}\mathit{MPa}\)
ultimate limit: \({\sigma}_{u}=\mathrm{820}\mathit{MPa}\)
The traction curve is as follows:
Table 1-2: Monotonous traction curve.
Deformity |
Constraint (\(\mathit{MPa}\)) |
0.002 |
\(\mathrm{330}\) |
0.0024 |
\(\mathrm{340}\) |
0.005 |
\(\mathrm{347}\) |
0.010 |
\(\mathrm{362}\) |
0.0198 |
\(\mathrm{404}\) |
0.0296 |
\(\mathrm{446}\) |
0.0392 |
\(\mathrm{484}\) |
0.0583 |
\(\mathrm{549}\) |
0.0770 |
\(\mathrm{609}\) |
0.1044 |
\(\mathrm{689}\) |
0.1222 |
\(\mathrm{742}\) |
0.1484 |
\(\mathrm{819}\) |
0.5000 |
\(\mathrm{820}\) |
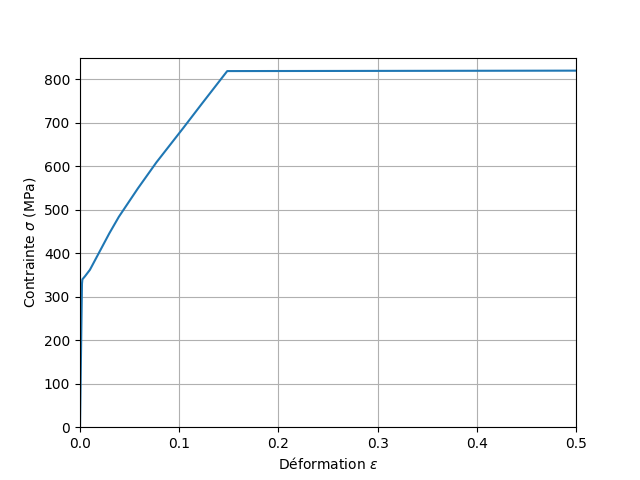
Fig. 1.2 Monotonic tensile curve of the elastoplastic law#
It was decided to model the elastoplastic behavior of Von Mises under isotropic work hardening, with this tension curve.
1.3. Loading conditions: trip 1#
The axial movement of the tube is blocked on the lower face of the model, and it is uniform and free on the upper face (unplugged tube).
The pressures exerted are chosen to be standardized by \(\mathit{h}/\mathit{R}\) in order to also be able to compare the mechanical behavior of the three tubes with each other for a similar load, presented in the following table:
Tube |
1 |
2 |
3 |
Ratio \(h/R\) |
0.05 |
0.10 |
0.20 |
Pressure \(Q\) (\(\mathit{MPa}\)) |
The successive values of the internal and external pressures and the stresses (we note \(\Delta P = P_{ext} - P_{int}\)) for path 1 are presented in the following tables:
Instant |
\(P_{int}\) |
\(P_{ext}\) |
0.5 |
\(Q/2\) |
\(0\) |
1.0 |
\(Q\) |
\(0\) |
2.0 |
\(2Q\) |
\(Q\) |
3.0 |
\(3Q\) |
\(3Q\) |
4.0 |
\(0\) |
\(Q\) |
5.0 |
\(0\) |
\(0\) |
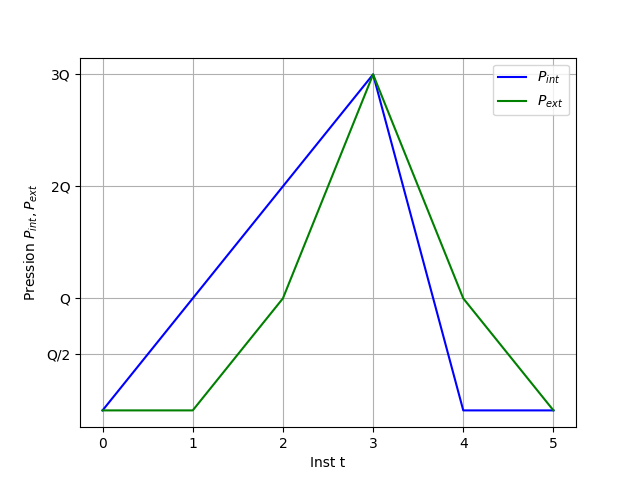
Fig. 1.3 Charging path 1#
Table 1-5: Steps, pressure differential and circumferential stresses according to the tubes (path 1) .
1.4. Loading conditions: trip 2#
The material is elastoplastic with isotropic work hardening with the traction curve including a perfect plastic tray, at \(330\mathit{MPa}\).
The axial movement of the tube is blocked on the lower face of the model, and it is uniform on the upper face (unplugged tube).
The pressure exerted on the inner wall, increasing monotonically to the point of collapse, is chosen to be normalized by \(\mathit{h}/\mathit{R}\) in order to also be able to compare the mechanical behavior of the three tubes with each other for a similar load. Ruin occurs when the entire thickness of the section is plasticized and the plastic tray reaches.
Instant |
\(P_{int}\) |
Tube 1 |
Tube 2 |
Tube 3 |
0.0 |
0.0 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
0.5 |
7.0 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
1.0 |
14.0 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
2.0 |
16.0 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
3.0 |
16.5 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
4.0 |
16.7 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |
5.0 |
16.71 |
\(\times 1\) |
\(\times 2\) |
\(\times 4\) |