1. Reference problem

The objective of this test case is to validate the 1D modeling of a cracked rotor (option ROTOR_FISS of DYNA_VIBRA) which simulates the behavior of a crack in a shaft line by an equivalent law.

The law is established thanks to 3D calculations carried out in a semi-static manner (see modeling D).

The results obtained by the « beam » and the crack element modeling are compared with the 3D calculation for extreme positions: closed crack and crack completely at most.

1.1. Geometry

For the cracked rotor, we consider a simple cylindrical straight beam with a length \(\mathrm{2L}\mathrm{=}4m\) and a diameter \(D\mathrm{=}\mathrm{0,8}m\). The crack is in the middle of the beam and has a straight bottom. The depth of the crack is 65%.

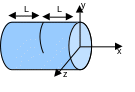
Figure 1: Cracked rotor geometry

1.2. Material properties

The rotor has a density of \(\rho =7800\mathrm{kg}/{m}^{3}\).

The Young’s modulus is \(E\mathrm{=}210{10}^{9}N{m}^{\mathrm{-}2}\) and the Poisson’s ratio is \(\nu \mathrm{=}\mathrm{0,3}\).

1.3. Boundary conditions and loads

For models A, B and C, the beam is embedded on the left and is subjected to a bending moment of unit amplitude according to \(Y\) on its right end. It is considered that the crack rotates relatively slowly at the speed \(5\) revolutions per second (\(300\text{rpm}\)).

For the D modeling, the boundary conditions imposed are on the one hand, an embedment in the sense of the theory of beams of one of the ends of the cylinder by means of a 3D- POU connection, and on the other hand, a unilateral contact without friction between the lips of the cracks. The imposed load is a unit bending moment of components \(({M}_{x},{M}_{y})\) applied at the free end. The orientation of this moment changes according to the moment of calculation.

1.4. Initial conditions

In the initial state, \(t=0\), the crack is closed. It is gradually opened by a linear ramp spread over \(0.2s\) leading the moment along \(Y\) from \(0\) to \(1\mathrm{Nm}\).