6. D modeling

6.1. Characteristics of modeling

As specified above, the characterization of the behavior of the cracked rotor requires the production of a three-dimensional model of a cracked beam in bi-axial bending.

This D modeling makes it possible to capitalize the meshing procedure for a standard cracked cylinder as well as the Python script to identify the laws characterizing the behavior of the cracked rotor studied in models A, B and C.

We consider a rotor element of Young’s modulus \(E\), of quadratic inertia \(I\) (identical in all directions of the plane of section) and of length \(2L\mathrm{=}4m\) and of diameter \(D\mathrm{=}1m\) containing in its median section a transverse crack with a right bottom of a depth of 65%.

Figure 6: single cracked specimen

A non-linear static calculation is performed with Code_Aster for 36 loading steps by changing the orientation \({\Phi }_{i}\) of the moment with a step of \(10°\) in order to cover the complete interval \(\mathrm{[}0°\mathrm{-}360°\mathrm{]}\). The post-processing is carried out by a Python script that uses the result file from Code_Aster. Based on the following rotations \(X\) and \(Y\) of the end of the cylinder under rotating loading imposed for each moment of calculation, the Python script makes it possible to calculate the deformation energy, the flexibility associated with the deformations of the cracked cylinder, the local stiffness as well as its derivative.

The dimensionless stiffness and derivative curves obtained depend on the orientation \(\Phi\) of the forces applied with respect to the angular position of the crack.

6.2. Characteristics of the mesh

The mesh contains 6315 knots and 6720 stitches.

Number of stitches POI1	17
Number of stitches SEG2	77
Number of stitches TRIA3	94
Number of stitches QUAD4	932
Number of stitches PENTA6	480
Number of stitches HEXA8	5120

6.3. Results: 1D crack behavior law

The law of behavior of the 1D crack is plotted in the figure below.

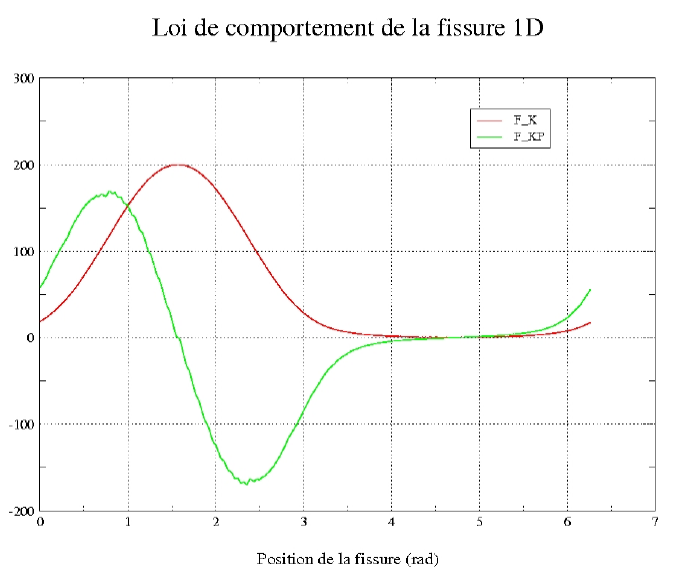
Figure 7: Law of behavior of the 1D crack