1. Reference problem#
1.1. Geometry#
We consider a plate with a height \(h=\mathrm{0,1}m\), a width \(l=\mathrm{0,05}m\) and a thickness \(e=0.005m\). A crack is positioned in the middle of the height of the beam, with a depth of \(\mathrm{0,1}l\) .
|
|
1.2. Material properties#
We consider the classical properties of a steel:
Young’s module: |
\(E={2.10}^{5}\mathrm{MPa}\) |
Poisson’s ratio: |
\(\nu =0.3\) |
Density |
\(\rho =7800\mathrm{kg}/{m}^{3}\) |
1.3. Boundary conditions and loads#
The plate is:
embedded on surface \({S}_{\mathrm{1 }}\);
subjected to a \(F(t)\) force on the \({S}_{2}\) surface.
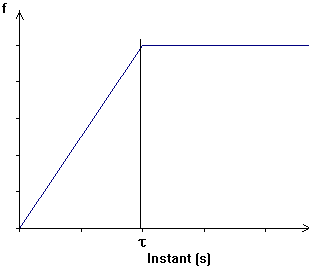
The evolution of the \(F(t)\) standard is shown in the figure above. We take \(\tau =\mathrm{0,001}s\). The direction of force \(F(t)\) is as follows:
\(F(t)=f(t)\mathrm{.}{e}_{x}\) for modeling A;
\(F(t)=(a{e}_{x}+b{e}_{y}+c{e}_{z})f(t)\) for B modeling, with \(b=\mathrm{2a}\) and \(c=0.4a\).
For modeling A, we block the movements in the \(z\) direction (plane problem).
