4. B modeling#
4.1. Characteristics of modeling#
It is a 3D model. The calculation of the evolution of stress intensity factors as a function of time is carried out in several stages:
calculation of the first 50 natural modes of the structure;
calculation of the intensity factors of the modal constraints associated with these modes by two methods;
resolution of the transitory dynamic problem by projection on a modal basis;
recombination of \(K\) modals.
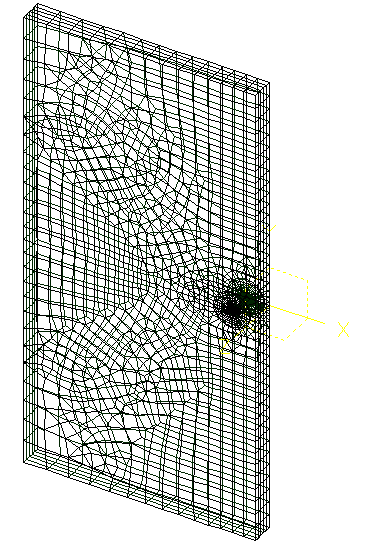
4.2. Characteristics of the mesh#
The mesh is composed of linear elements. It has 8200 knots and 8900 stitches and is refined around the crack bottom.
4.3. Tested sizes and results#
The values shown are those found at the node that is in the middle of the crack bottom.
Modal values: non-regression test case
Mode Number |
\({K}_{I}\) ( POST_K1_K2_K3 )) ** |
:math:`{K}_{I}`** (K**** option) ** |
% difference |
|
1 |
5,631E+09 |
4,790E+09 |
14,9 |
|
2 |
8,599E+09 |
7,291E+09 |
15,2 |
|
3 |
6,940E+10 |
5,897E+10 |
15,0 |
|
4 |
-2,702E+11 |
-2,897E+11 |
-2,702E+11 |
-7,2 |
5 |
-9,637E+10 |
-8,165E+10 |
15,3 |
Time values \({K}_{I}(t)\) : comparison to explicit resolution
Instant ( \(s\) ) |
Reference ( \(\mathrm{Pa.}\sqrt{m}\) ) |
Aster ( \(\mathrm{Pa.}\sqrt{m}\) ) |
% difference |
0.0005 |
696752.4 |
721825.9 |
3.6 |
0.001 |
1153703.3 |
1239061.8 |
7.4 |
0.002 |
997675,6 |
1110569,6 |
11,3 |
0.003 |
1305429.9 |
1364524.8 |
4.5 |
0.004 |
870347.2 |
1004735.2 |
15.4 |
4.4. note#
The difference between the modal values calculated by interpolation of displacement jumps or by the theta method is high: this is explained by the very unrefined linear mesh in the thickness of the plate.
The value of \({K}_{I}(t)\) is calculated from the modal \({K}_{I}\) (optionK) and the resolution coefficients on a modal basis directly in the command line test case in python:
\({K}_{I}(s,t)=\underset{i=1}{\overset{M}{\Sigma }}{\alpha }_{i}\mathrm{.}{K}_{I}^{i}(s)\)
where the coefficients \({\alpha }_{i}(t)\) are the modal participation coefficients, extracted from the result of the DYNA_VIBRA operator, and the \({K}_{I}^{i}(s)\) are the intensity factors of the modal constraints.
The precision obtained is satisfactory considering the number of elements retained in the modal base (50) and the size of the mesh. Precision increases rapidly with the number of modes [bib1].