7. Parallelization

Parallelization in MULT_FRONT is done by Openmp directives. These guidelines are placed in the following routines:

Symmetric real case: MLTFMJ, MLTFLJ

Symmetric complex case: MLTCMJ, MLTCLJ

Non-symmetric real case: MLNFMJ, MLNFLJ

Complex non-symmetric case: MLNCMJ, MLNCLJ

The parallelization implemented is « said » internal, it takes place within the process of eliminating a supernode. The elimination of supernodes, called « external » ones, can also be parallelized. But it is not implemented for the following reason: The simultaneous elimination of several supernodes requires more memory than the sequential version. However, the concern for memory occupancy has always predominated that of saving rendering time during the previous developments of MULT_FRONT.

Internal parallelization does not require any additional memory than the sequential version, nor does it require any special code development, only the simple addition of directives.

We will describe the parallelization of routine MLTFMJ, that of MLTFLJ follows the same principles, as well as the other routines mentioned above.

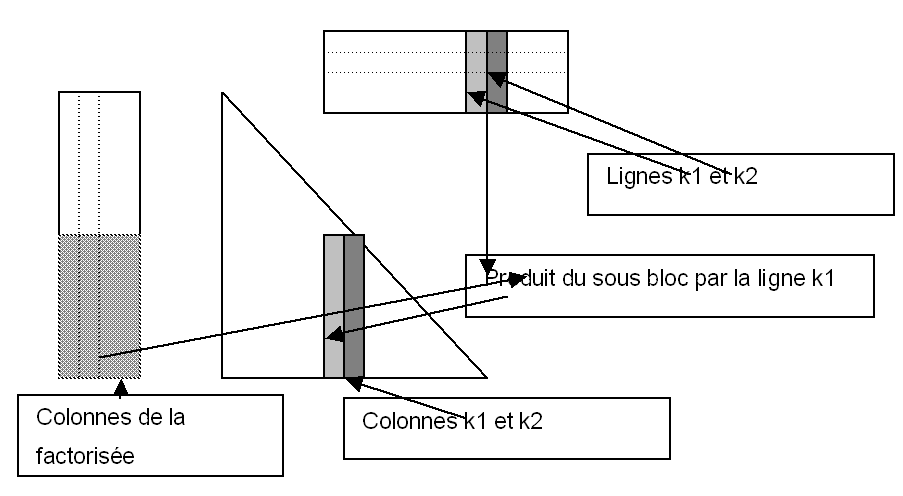
Figure 9 Front Matrix Update Diagram

The figure above shows a diagram of how the front-end matrix is updated when a node is eliminated. The triangle represents the lower part of the front matrix, and the 2 rectangles represent the columns of the factored matrix, columns corresponding only to the supernode eliminated. At first, we will reason by columns. We know that column \(\mathit{k1}\) of the front matrix is updated by subtracting from it the product of the sub-block of columns (shaded above) by row \(\mathit{k1}\) (multiplied by the diagonal terms itself). (Blas2 operation). This update operation is parallelized without problems by an OpenMP directive, the columns of the front-end matrix are adjacent, there is no conflict of addresses. All variables are shared except loop indices and local variables. We saw above that for the sake of performance, one works by block of columns, in order to use Blas3, the parallelization mentioned above is therefore in fact carried out on the blocks of columns and not on the columns themselves.

Code Overview:

C$ OMP PARALLEL DO DEFAULT (PRIVATE)

C$ OMP + SHARED (N, M, P, P, NMB,,,, NB, NB, RESTM, FRONT, ADPER, DECAL, FRN,, TRAV, C)

C$ OMP + SHARED (TRA, TRB, ALPHA, BETA)

C$ OMP + SCHEDULE (STATIC ,1)

DO 1000 KB = 1, NMB

NUMPRO = MLNUMP ()

C K: INDICE FROM COLONNE DANS THE MATRICE FRONTALE (ABSOLU FROM 1 TO N)

K = NB* (KB-1) + 1 +P

DO 100 I=1, P

S = FRONT (ADPER (I))

ADD = N* (I-1) + K

DO 50 J=1, NB

TRAV (I, J, NUMPRO) = FRONT (ADD) *S! TRAV contains the products: diagonal*line term

ADD = ADD + 1

50 CONTINUE

100 CONTINUE

DO 500 KB = KB, NMB

IA = K + NB* (IB-KB)

IT=1

CALL DGEMM (TRA, TRB, NB, NB, P, P, ALPHA, FRONT (IA), N,

& TRAV (IT,1, NUMPRO), P, BETA, C (1,1, NUMPRO), NB)

C RECOPIE

C

DO 501 I=1, NB

I1=I-1

IF (IB.EQ.KB) THEN

J1= I

IND = ADPER (K + I1) - DECAL

ELSE

J1=1

IND = ADPER (K + I1) - DECAL + NB* (IB-KB) - I1

ENDIF

DO 502 J=J1, NB

FRN (IND) = FRN (IND) +C (J, I, NUMPRO)! Copy into the frn front matrix

IND = IND +1

502 CONTINUE

501 CONTINUE

500 CONTINUE

1000 CONTINUE

C$ OMP END PARALLEL DO

N.B. Parallelization.

The sequential version requires a work board \(\mathit{TRA}\) , written for each block, it is necessary to duplicate it for parallelization. In the parallel loop, we call the function MLNUMPqui provides the thread number processing the loop iteration; NUMPRO, we then work in the plan NUMPROdu array \(\mathit{TRAV}\).