1. Reference problem#
1.1. Geometry#
We consider an infinite hollow cylinder.
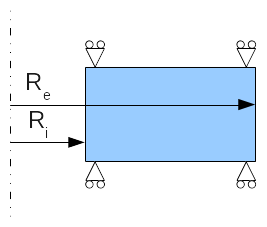
Figure 1: Hollow cylinder geometry
Modeling A:
The geometric properties are:
Inner radius \({R}_{i}\mathrm{=}10\mathit{mm}\)
External radius \({R}_{e}\mathrm{=}20\mathit{mm}\)
B modeling:
The geometric properties are:
Inner radius \({R}_{i}\mathrm{=}100\mathit{mm}\)
External radius \({R}_{e}\mathrm{=}200\mathit{mm}\)
1.2. Material properties#
The materials used in the calculations use the VMIS_JOHN_COOK law of behavior. Its work hardening function is written as follows [1]:
\(R(p,\dot{p},T)\mathrm{=}(A+B{p}^{n})(1+C\mathrm{ln}(\frac{\dot{p}}{\dot{{p}_{0}}}))(1\mathrm{-}(\frac{T\mathrm{-}{T}_{\mathit{room}}}{{T}_{\mathit{melt}}\mathrm{-}{T}_{\mathit{room}}}))\)
We will not use terms related to temperature dependence and the rate of plastic deformation. We will then work with:
\(R(p)\mathrm{=}A+B{p}^{n}\)
Modeling A:
An elastic law of behavior is modelled. The following mechanical and thermal parameters are used:
Young’s module \(E\mathrm{=}206900\mathit{MPa}\)
Poisson’s ratio \(\nu \mathrm{=}0.29\)
Elastic limit \(A\mathrm{=}5{.10}^{100}\mathit{Pa}\)
Post-elastic slope \(B\mathrm{=}2{.10}^{10}\mathit{Pa}\)
Post-elastic power \(n\mathrm{=}1\)
Density \(\rho \mathrm{=}7800\mathit{kg}\mathrm{/}{m}^{3}\)
Expansion coefficient \(\alpha \mathrm{=}\mathrm{1,5}{.10}^{\mathrm{-}5}{K}^{\mathrm{-}1}\)
Conductivity \(\lambda \mathrm{=}45W\mathrm{/}(\mathit{m.K})\)
Heat capacity \({C}_{p}\mathrm{=}460J\mathrm{/}(\mathit{kg.K})\)
Reference temperature \({T}_{\mathit{ref}}\mathrm{=}293K\)
B modeling:
An elastoplastic behavior law equivalent to a VMIS_ISOT_LINE law is modelled. The following mechanical and thermal parameters are used:
Young’s module \(E\mathrm{=}70000\mathit{MPa}\)
Poisson’s ratio \(\nu \mathrm{=}0.3\)
Yield strength as a function of temperature \(A(T)\mathrm{=}A({T}_{\mathit{ref}})(1\mathrm{-}w(T\mathrm{-}{T}_{\mathit{ref}}))\)
Yield strength at reference temperature \(A({T}_{\mathit{ref}})\mathrm{=}70\mathit{MPa}\)
Linear softening coefficient \(w\mathrm{=}3{.10}^{\mathrm{-}4}{K}^{\mathrm{-}1}\)
Post-elastic slope \(B\mathrm{=}210\mathit{MPa}\)
Post-elastic power \(n\mathrm{=}1\)
Density \(\rho \mathrm{=}2700\mathit{kg}\mathrm{/}{m}^{3}\)
Expansion coefficient \(\alpha \mathrm{=}\mathrm{2,38}{.10}^{\mathrm{-}5}{K}^{\mathrm{-}1}\)
Conductivity \(\lambda \mathrm{=}150W\mathrm{/}(\mathit{m.K})\)
Heat capacity \({C}_{p}\mathrm{=}900J\mathrm{/}(\mathit{kg.K})\)
Reference temperature \({T}_{\mathit{ref}}\mathrm{=}293K\)
1.3. Boundary conditions and loads#
Modeling A:
A radial displacement of \(20\mathit{mm}\) is imposed on the inner face of the cylinder at the speed of \(\mathrm{1mm}\mathrm{/}s\). The temperature of the external face is set to \({T}_{\mathit{ref}}\). The other faces of the cylinder are considered to be thermally insulated. The behavior is thermoelastic and the expansion of a cylinder therefore causes it to cool.
B modeling:
The surface of the cylinder is considered to be thermally insulated. The displacement of the inner face of the cylinder is \(130\mathit{mm}\) applied in \(\mathrm{1,3}s\). The behavior is thermoelastoplastic and the plastic dissipation effect compensates for the previous thermo-elastic cooling effect to cause the overall heating of the cylinder.
1.4. Initial conditions#
The cylinder temperature is equal to \({T}_{\mathit{ref}}\).