1. Reference problem#
1.1. Geometry#
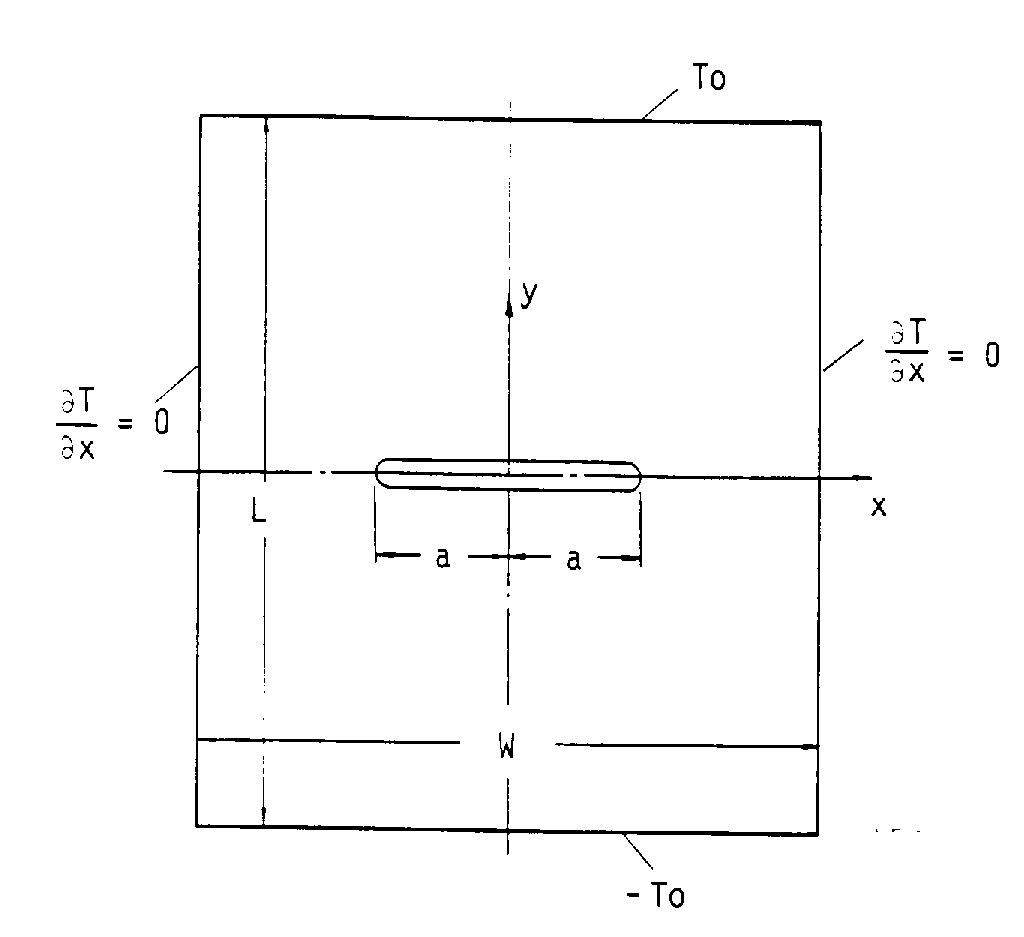
Plate width: |
\(W\mathrm{=}0.6m\) |
Plate length: |
\(L=0.3m\) |
Crack length: |
\(\mathrm{2a}=0.3m\) |
1.2. Material properties#
Rating for thermoelastic properties:
\(\left\{\begin{array}{c}{\varepsilon }_{x}\\ {\varepsilon }_{y}\\ {\gamma }_{\mathit{xy}}\end{array}\right\}\mathrm{=}\left[\begin{array}{ccc}{S}_{11}& {S}_{12}& 0\\ {S}_{12}& {S}_{22}& 0\\ 0& 0& {S}_{66}\end{array}\right]\left\{\begin{array}{c}{\sigma }_{x}\\ {\sigma }_{y}\\ {\tau }_{\mathit{xy}}\end{array}\right\}+\left\{\begin{array}{c}{\alpha }_{11}\\ {\alpha }_{22}\\ 0\end{array}\right\}\mathrm{\cdot }(T\mathrm{-}{T}_{\mathit{ref}})\)
\(\begin{array}{c}{S}_{11}\mathrm{=}1\mathrm{/}{E}_{x}\\ {S}_{22}\mathrm{=}1\mathrm{/}{E}_{y}\\ {S}_{12}\mathrm{=}\mathrm{-}{\nu }_{x}\mathrm{/}{E}_{x}\mathrm{=}\mathrm{-}{\nu }_{y}\mathrm{/}{E}_{y}\\ {S}_{66}\mathrm{=}1\mathrm{/}{G}_{\mathit{xy}}\\ {\alpha }_{11}\mathrm{=}{\alpha }_{x}\\ {\alpha }_{22}\mathrm{=}{\alpha }_{y}\end{array}\)
We are limited to isotropic material, both from a thermal and mechanical point of view:
\({E}_{x}\mathrm{=}{E}_{y}\mathrm{=}2.{10}^{5}\mathit{MPa}\)
\({\nu }_{x}\mathrm{=}{\nu }_{y}\mathrm{=}0.3\)
\({\alpha }_{x}\mathrm{=}{\alpha }_{y}\mathrm{=}1.2{10}^{\mathrm{-}5}°{C}^{\mathrm{-}1}\)
\({\lambda }_{x}\mathrm{=}{\lambda }_{y}\mathrm{=}54.W\mathrm{/}m°C\)
1.3. Boundary conditions and loading#
Two models are considered:
the half-model \(x=0\)
the complete model
Mechanical boundary conditions:
half-model
\(\mathrm{UX}=0\) along the axis of symmetry \(X=0\)
\(\mathrm{UY}=0\) in focus (\(W/2.\))
full model
\(\mathrm{UX}=0\) at point \((\mathrm{0,}L/2.)\)
\(\mathrm{UY}=0\) at points \((-L/2.)\) and \((L/2.)\)
Thermal boundary conditions:
half-model
\(T=100°C\) on the top edge \(Y=L/2\).
\(T=-100°C\) on the bottom edge \(Y=-L/2\).
zero flow on the axis of symmetry, on the free edge \(X=W/2.\) and on the edge of the crack
full model
\(T\mathrm{=}100°C\) on the top edge \(Y=L/2\).
\(T\mathrm{=}\mathrm{-}100°C\) on the bottom edge \(Y=-L/2\).
zero flux on free edges \(X\mathrm{=}\mathrm{\pm }W\mathrm{/}2.\) and on the edge of the crack