1. Reference problem#
1.1. Geometry#
Consider a rectangle of length \(325m\) and width \(10m\) in plane \((\mathrm{0,}X,Y)\).
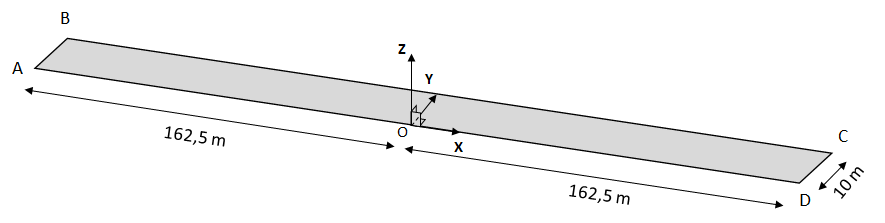
The thickness of the membrane is entered in AFFE_CARA_ELEM via the keyword EPAIS and is equal to \(e={\mathrm{2,2783.10}}^{-5}m\). This thickness is chosen so as to obtain a mass equal to that used in test case SSNL114, at an identical density.
1.2. Material properties#
The material is hyperelastic, almost incompressible, isotropic, whose properties are:
\(E=57000\mathit{MPa}\)
\(\mathrm{\nu }=0.49\)
\(\mathrm{\rho }=2\mathrm{844,23}\mathit{kg}/{m}^{3}\)
We use Saint Venant Kirchhoff’s law of behavior.
1.3. Boundary conditions and loads#
On edges \(\mathit{AB}\) and \(\mathit{CD}\): \(\mathit{DX}=0\), \(\mathit{DZ}=0\).
On edge \(\mathit{AD}\): \(\mathit{DY}=0\).
Gravity is applied to the entire model, it is worth \(g=\mathrm{9,81}m/{s}^{2}\) and is oriented according to (0,0, -1) in the \((X,Y,Z)\) coordinate system.
The non-following pressure is applied to the entire model, it is worth \(p\text{}=\text{}\mathrm{\rho }\ast e\ast g\text{}\approx \text{}\mathrm{0,6357}\mathit{Pa}\) and is oriented according to \((\mathrm{0,0,}-1)\) in the coordinate system \((X,Y,Z)\).
The two loads are treated separately.
1.4. Initial conditions#
An initial voltage of \(10\mathit{MPa}\) is entered in AFFE_CARA_ELEM using the N_ INIT keyword. This tension disappears after the first Newton increment.