1. Reference problem#
1.1. Geometry#
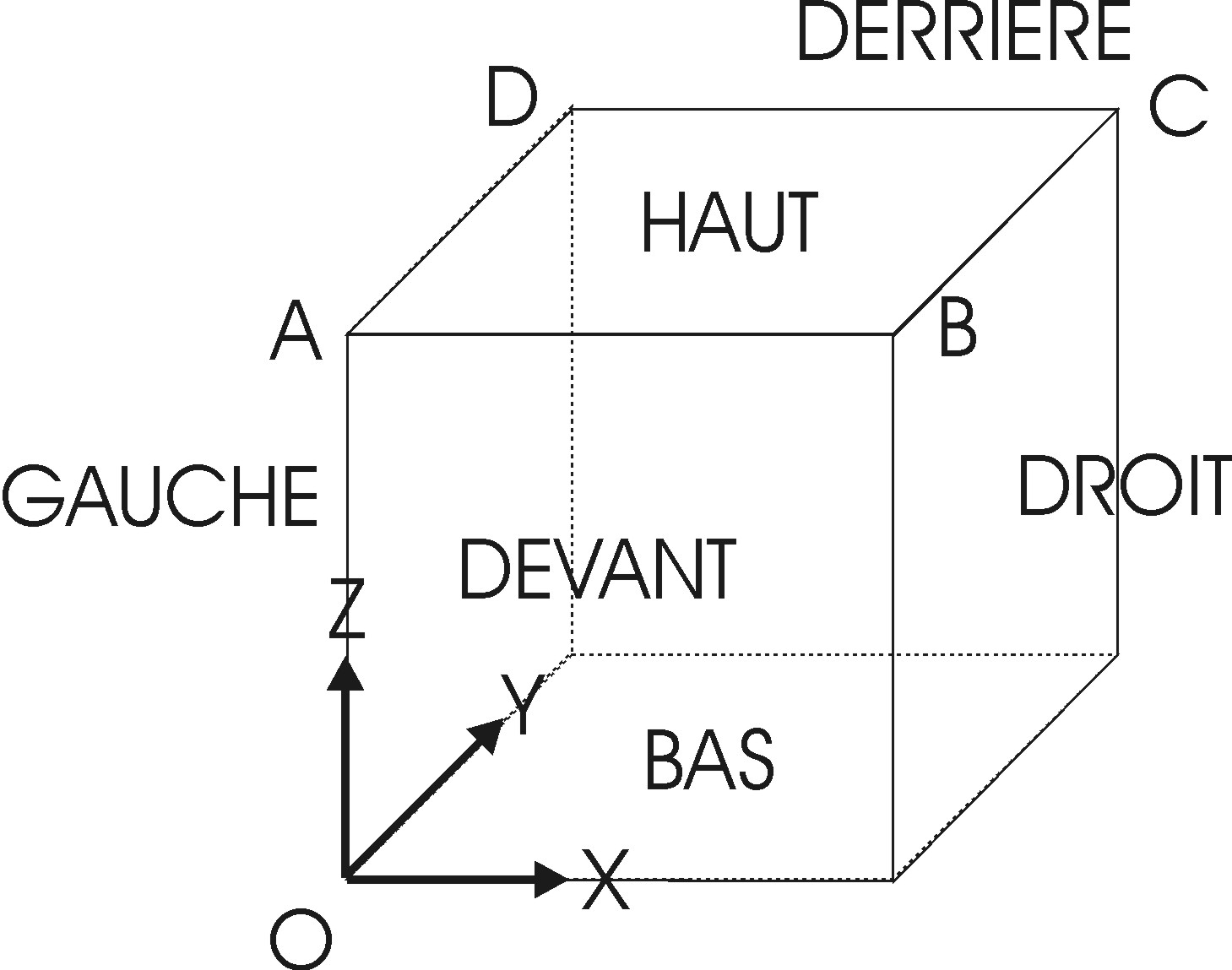
The simple tensile test is carried out on a single isoparametric finite element of cubic shape \(\mathit{CUB}4\). The length of each edge is 1. The different facets of this cube are mesh groups named \(\mathrm{HAUT}\), \(\mathrm{BAS}\),, \(\mathrm{DEVANT}\), \(\mathrm{DERRIERE}\), \(\mathrm{DROIT}\), and \(\mathrm{GAUCHE}\). The mesh group SYM also contains the mesh groups \(\mathrm{BAS}\), \(\mathrm{DEVANT}\) and \(\mathrm{GAUCHE}\); the group of elements \(\mathrm{COTE}\) the mesh groups \(\mathrm{DERRIERE}\) and \(\mathrm{DROIT}\).
1.2. Material properties#
The elastic properties are:
Young’s modulus: \(E=1\mathit{MPa}\)
Poisson’s ratio: \(\mathrm{\nu }=\mathrm{0,25}\)
The traction limit is equal to \({\mathrm{\sigma }}_{t}=1\mathit{kPa}\)
1.3. Boundary conditions and loads#
The simple tensile test consists in imposing a vertical elongation on the specimen while maintaining the lateral pressure constant and equal to the initial isotropic stress \({P}_{0}=10\mathit{kPa}\)
In the model under consideration, the cubic element represents one eighth of the sample. The boundary conditions are therefore as follows:
Symmetry conditions:
\({u}_{z}=0\) on mesh group \(\mathrm{BAS}\)
\({u}_{x}=0\) on mesh group \(\mathrm{GAUCHE}\)
\({u}_{y}=0\) on mesh group \(\mathrm{DEVANT}\)
Lateral pressure conditions:
\({P}_{n}={P}_{0}=10\mathit{kPa}\) on mesh groups \(\mathit{DROIT}\) and \(\mathit{ARRIERE}\)
Loading conditions:
\({u}_{z}=+1\) on mesh group \(\mathrm{HAUT}\)
The loading takes place in 30 steps of time between \(t=0\) and \(t=30\) during which the displacement imposed on the group of elements \(\mathrm{HAUT}\) varies from \({u}_{z}=0\) to \({u}_{z}=0.3\) (total vertical deformation of \(30\text{\%}\)).
1.4. Results#
The solutions are post-treated at point \(C\), in terms of:
vertical constraint \({\mathrm{\sigma }}_{\mathit{zz}}\);
horizontal deformation \({\mathrm{ϵ}}_{\mathit{xx}}\);
\({e}^{P}=\Vert {e}^{P}\Vert\) deviatoric plastic deformation norm
They are compared to an analytical solution (described in the next paragraph) in terms of maximum difference between \(t=0\) and \(t=20\).