1. Reference problem#
1.1. Geometry of the problem#
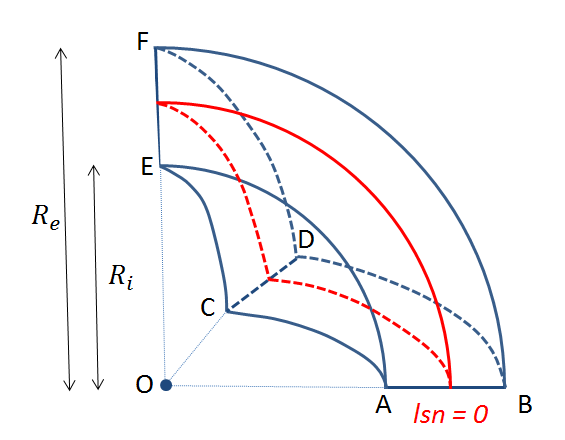
It is one-eighth of a sphere with inner radius \({R}_{i}=1m\), outer radius \({R}_{e}=2m\), and center \(O(\mathrm{0,0}\mathrm{,0})\). This portion of the sphere is crossed by an interface-type discontinuity (a non-meshed interface that is introduced into the model through level-sets using the DEFI_FISS_XFEM operator), concentric with radius \(R=\mathrm{1.5m}\).
The geometry of the column is shown in the figure.
1.2. Material properties#
The parameters given in the Table correspond to the parameters used for the 4 models. The behavior is elastic (“ELAS”).
Elastic parameters |
Young’s modulus \(E(\mathit{en}\mathit{MPa})\) Poisson’s ratio \(\nu\) Thermal expansion coefficient \(\alpha (\mathit{en}{K}^{\text{-1}})\) |
\(0\) \(0\) |
Table 1.2-1 : Material Properties
1.3. Boundary conditions and loading#
The following Dirichlet conditions apply:
on the lower face [ABDC], the movements following \(z\) are blocked \({u}_{\text{z}}=0\),
on the [ABFE] side, the movements following \(y\) are blocked \({u}_{\text{y}}=0\),
on the [CDFE] side, the movements following \(x\) are blocked \({u}_{\text{x}}=0\),
on outer shell BDF and inner shell ACE, movements are blocked in all directions (\({u}_{\text{x}}=0\), \({u}_{\text{y}}=0\) and \({u}_{\text{z}}=0\)).
The load is as follows:
On each of the lips of the interface at \(r=R\) a uniform distributed pressure is imposed \(p=10\mathit{MPa}\) by means of AFFE_CHAR_MECA and the keyword FISSUREdePRES_REP.