1. Reference problem#
1.1. Geometry of the problem#
It is a column with height \(\mathit{LZ}=5m\), length \(\mathit{LX}=1m\), and width \(\mathit{LY}=1m\). In \(Z={L}_{d}\), this column has an interface-type discontinuity (a non-meshed interface that is introduced into the model through level-sets using the DEFI_FISS_XFEM operator). The column is thus entirely crossed by the discontinuity (in terms of approximating the displacement field, only Heaviside enrichment is taken into account). The height of the \(Y={L}_{d}\) interface will be different in the c and d models.
The geometry of the column is shown in the figure.
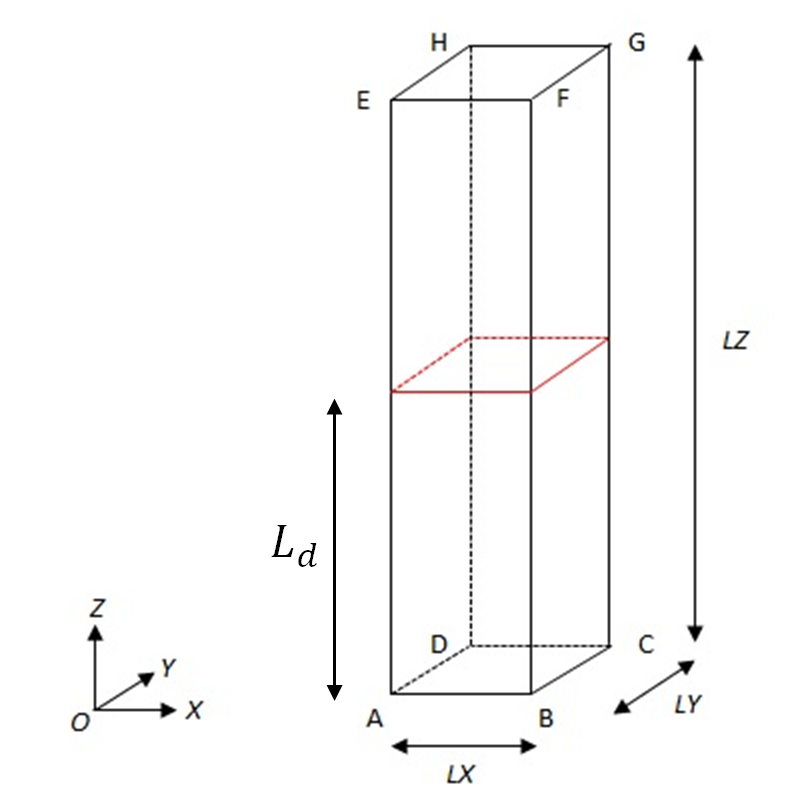
Figure 1.1-a : Problem geometry 3D
1.2. Material properties#
Young’s module: \(E=5800\mathit{MPa}\)
Poisson’s ratio: \(\nu =0\)
Coefficient of thermal expansion: \(\alpha =0{K}^{\text{-1}}\)
1.3. Boundary conditions#
2D case
The boundary conditions that are applied are of the Neuman type. We impose:
Across the field \({u}_{y}(x,y)={f}_{y}(x,y)\) with \({f}_{y}(x,y)=\{\begin{array}{c}-0.01\ast y\mathit{si}Y<{L}_{d}\\ 0.01\ast (\mathit{LY}-y)\mathit{si}Y>{L}_{d}\end{array}\)
On the [AD] \({u}_{x}(x,y)={f}_{\mathit{null}}\) side with \({f}_{\mathit{null}}\) the zero value constant function
On the side [BC] \({u}_{x}(x,y)={f}_{x}(x,y)\)
In modeling A (linear) \({f}_{x}(x,y)=\{\begin{array}{c}0.01\ast y\mathit{si}Y<{L}_{d}\\ -0.01\ast (\mathit{LY}-y)\mathit{si}Y>{L}_{d}\end{array}\)
In B modeling (quadratic) \({f}_{x}(x,y)=\{\begin{array}{c}0.01\ast {y}^{2}\mathit{si}Y<{L}_{d}\\ -0.01\ast {(\mathit{LY}-y)}^{2}\mathit{si}Y>{L}_{d}\end{array}\)
3D case
The boundary conditions that are applied are of the Neuman type. We impose:
Across the field \({u}_{z}(x,y,z)={f}_{z}(x,y,z)\) with \({f}_{z}(x,y,z)=\{\begin{array}{c}-0.01\ast z\mathit{si}Z<{L}_{d}\\ 0.01\ast (\mathit{LZ}-z)\mathit{si}Z>{L}_{d}\end{array}\)
On the [ADEH] \({u}_{x}(x,y,z)={f}_{\mathit{null}}\) face with \({f}_{\mathit{null}}\) the zero value constant function
On the face [BCGF] \({u}_{x}(x,y,z)={f}_{x}(x,y,z)\)
In C modeling (linear) \({f}_{x}(x,y,z)=\{\begin{array}{c}0.01\ast z\mathit{si}Z<{L}_{d}\\ -0.01\ast (\mathit{LZ}-z)\mathit{si}Z>{L}_{d}\end{array}\)
In D modeling (quadratic) \({f}_{x}(x,y,z)=\{\begin{array}{c}0.01\ast {z}^{2}\mathit{si}Z<{L}_{d}\\ -0.01\ast {(\mathit{LZ}-z)}^{2}\mathit{si}Z>{L}_{d}\end{array}\)
Throughout the \({u}_{y}(x,y,z)={f}_{\mathit{null}}\) domain