6. D modeling#
6.1. Characteristics of modeling#
POU_D_TGM (multi-fiber 3D beam for nonlinear geometric and material analysis).
6.2. Characteristics of the mesh#
Number of knots: 11
Number of meshes and type: 10 SEG2
6.3. Characteristics of the cross section mesh#
Number of fibers: 160 (40 in thickness and 4 in width)
Number of meshes and type: 160 QUAD4
6.4. Tested sizes and results#
The incremental analysis is carried out in the pseudo-time interval \(\mathrm{[}\mathrm{0 }\mathrm{:}6\mathrm{]}\) in 1200 load steps.
6.4.1. History of horizontal rotation \(\text{DRY}\) (radians) at loaded nodes#
Instant |
Moment \(m\) |
Reference Type |
Reference |
Tolerance (%) |
0.3 |
“ANALYTIQUE” |
—0.3000E+00 |
0.1 |
|
0.6 |
“ANALYTIQUE” |
—0.6000E+00 |
0.1 |
|
1.0 |
“ANALYTIQUE” |
—1.0000E+00 |
0.1 |
|
3.0 |
“ANALYTIQUE” |
—3.0000E+00 |
0.1 |
|
6 |
600 |
“ANALYTIQUE” |
—6.0000E+00 |
0.1 |
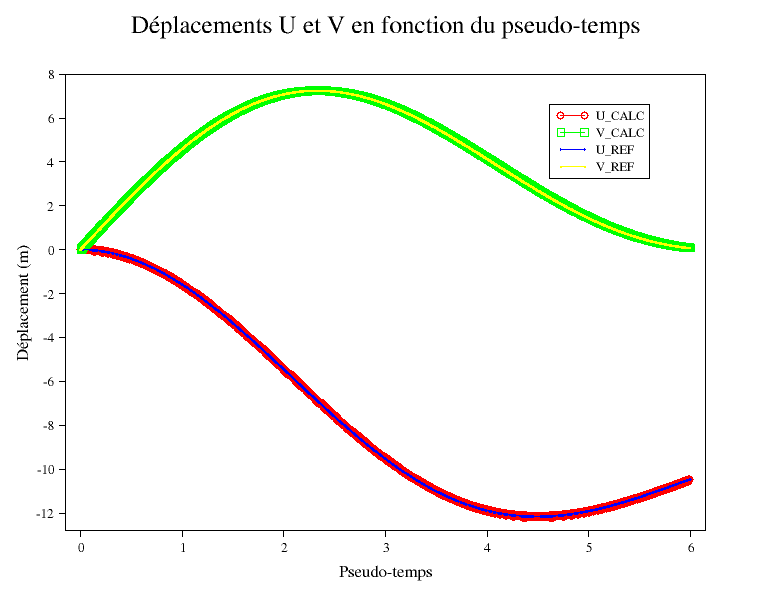
6.4.2. History of horizontal displacement \(\text{DX}(\text{m})\) at loaded nodes#
Instant |
Moment \(m\) |
Reference Type |
Reference |
Tolerance (%) |
0.3 |
“ANALYTIQUE” |
—1.4932E-01 |
2.0 |
|
0.6 |
“ANALYTIQUE” |
—5.8934E-01 |
1.0 |
|
3.0 |
“ANALYTIQUE” |
—9.5296 |
0.3 |
|
6 |
600 |
“ANALYTIQUE” |
—10.4657 |
0.3 |
6.4.3. History of vertical displacement \(\text{DZ}(\text{m})\) at loaded nodes#
Instant |
Moment \(m\) |
Reference Type |
Reference |
Tolerance (%) |
0.3 |
“ANALYTIQUE” |
1.4887E+00 |
0.1 |
|
0.6 |
“ANALYTIQUE” |
2.9110E+00 |
0.1 |
|
3.0 |
“ANALYTIQUE” |
6.6333 |
0.5 |
|
6 |
600 |
“ANALYTIQUE” |
6.638286E-02 |
0.07 |
At the last step of time, the vertical displacement is very low compared to the maximum achieved during the loading path (\(\text{DZ}\) maximum around \(7\text{m}\)). A relative comparison with the reference solution is not very relevant (there would then be almost 30% relative error). We would prefer a test in relation to the maximum displacement: \(\frac{\mathrm{valeur}\mathrm{calculée}-\mathrm{valeur}\mathrm{de}\mathrm{référence}}{{\mathrm{DZ}}_{\mathrm{max}}}<{\mathrm{tol}}^{\mathrm{relative}}\).
To do this, we test in absolute terms, with an absolute tolerance equal to \({\mathrm{DZ}}_{\mathrm{max}}\mathrm{.}{\mathrm{tol}}^{\mathrm{relative}}\).