3. B modeling

3.1. Characteristics of modeling

A modeling testing the functionalities of contact with friction treated with the penalization method was implemented. Given the symmetry of the problem, it comprises a quarter of the ring as well as the mesh of a non-deformable plate.

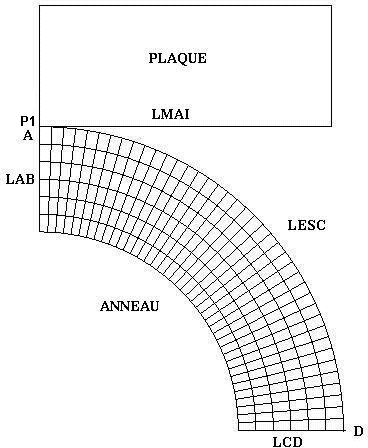
Boundary condition:

Symmetry conditions:

the nodes of group \(\mathrm{LAB}\) located in the plane \(X=0\) are blocked in the direction \(X\) (\(\mathrm{DX}=0\)), the nodes of the group \(\mathrm{LCD}\) located in the plane \(Y=0\) are blocked in the direction \(Y\) (\(\mathrm{DY}=0\)), all the nodes in mesh group \(«\mathrm{Plaque}»\) are blocked in the direction \(X\) (\(\mathrm{DX}=0\))

To avoid rigid body movements, nodes \(A\) and \(\mathrm{P1}\) even move vertically.

Loads:

Imposed displacement following \(Y\) on all nodes of the plate: \(\mathrm{DY}\) varies from \(0\) to \(\mathrm{2,225}\mathrm{cm}\).

(the value of \(\mathrm{4,45}\mathrm{cm}\) is the vertical approximation of the two symmetric plates.)

Note:

The mesh was made in \(\mathrm{cm}\) .

3.2. Characteristics of the mesh

Number of knots: 291

Number of meshes and type: 241 QUAD4 and 51 SEG2

3.3. Tested sizes and results

3.4. notes

The influence of friction can be visualized by looking at the shear stress at the nodes in contact. You have to differentiate between \(\mathrm{SIXY}\) with friction and \(\mathrm{SIXY}\) without friction to eliminate averaging problems on edge knots.