1. Reference problem#
1.1. Geometry and boundary conditions#
In these tests, a concrete plate (\(200\mathrm{\times }200\mathrm{\times }50\mathit{mm}\)) is subjected to a loading where the main stress ratio \({\sigma }_{2}\mathrm{/}{\sigma }_{1}\) is fixed (\({\sigma }_{3}\mathrm{=}0\)). These tests are modelled in two dimensions under the condition of plane constraints (\({\sigma }_{\mathit{zz}}\mathrm{=}0\)) using a quadrangle element with 4 nodes (QUAD4).
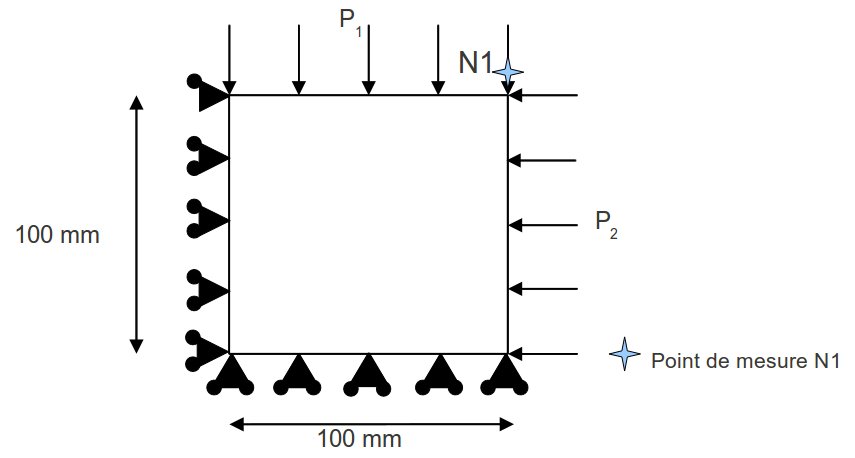
Figure 1.1-a: 2D modeling and boundary conditions for biaxial tests
Only a quarter of the concrete plate is modelled. Thus, symmetry conditions are imposed:
The following moves \(y\) are stuck on the bottom edge.
The following moves \(x\) are stuck on the left edge.
Two pressures are imposed on the free edges: \({P}_{1}\) and \({P}_{2}\). The relationship between the loads, and implicitly on the main constraints, is noted \(\omega\):
\({\mathrm{\sigma }}_{2}=\mathrm{\omega }{\mathrm{\sigma }}_{1}\) (Eq.1)
These pressures follow a linear law of evolution.
Instant |
0 |
1 |
\({P}_{1}\) (\(\mathit{MPa}\)) |
0 |
30 |
\({P}_{2}\) (\(\mathit{MPa}\)) |
0 |
|
Table 1.1-1 : Evolution of pressures
1.2. Material properties#
For the MAZARS model, the following parameters were used:
Elastic behavior:
\(E\mathrm{=}\text{34}\text{000}\text{MPa},\nu \mathrm{=}0\text{.}19\)
Damaging behavior:
\({\varepsilon }_{\mathit{d0}}\mathrm{=}1\text{.}\text{1}\text{.}{\text{10}}^{\mathrm{-}3};\text{Ac}\mathrm{=}1\text{.}\text{25};\text{At}\mathrm{=}1\text{.}0;\text{Bc}\mathrm{=}\text{1965};\text{Bt}\mathrm{=}\text{9}\text{000};k\mathrm{=}0\text{.}\text{7}\)
These material parameters induce a compression limit \({f}_{c}\) of the order of \(33\mathit{MPa}\).
1.3. Initial conditions#
Néant