1. Reference problem#
1.1. Geometry#
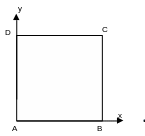
Size of the square: \(\mathrm{1m}\mathrm{\times }\mathrm{1m}\).
1.2. Material properties#
Elastic
\(E=5800.0\mathrm{E6}\mathrm{Pa}\) Young’s module
\(\nu =0.3\) Poisson’s Ratio
DRUCK_PRAGER with linear negative work hardening
\(\alpha \mathrm{=}0.33\) Pressure Dependence Coefficient
\({p}_{\mathrm{ultm}}=0.01\) Ultimate cumulative plastic deformation
\({\sigma }^{Y}=2.57\mathrm{E6}\mathrm{Pa}\) Plastic constraint
\(h=-2.\mathrm{E8}\mathrm{Pa}\) Work hardening module
DRUCK_PRAGER with parabolic negative work hardening
\(\alpha =0.33\) Pressure Dependence Coefficient
\({p}_{\mathrm{ultm}}=0.01\) Ultimate cumulative plastic deformation
\({\sigma }^{Y}=2.57\mathrm{E6}\mathrm{Pa}\) Plastic constraint
\({\sigma }_{\mathrm{ultm}}^{Y}=0.57\mathrm{E6}\mathrm{Pa}\) Ultimate constraint
1.3. Boundary conditions and loads#
The boundary conditions and loads applied are as follows:
Imposed loads: loads are constant \(t\mathrm{\in }\text{]}\mathrm{1,2}\mathrm{.}\text{]}\)
Side \(\mathrm{BC}\) \(p={2.10}^{6}\mathrm{Pa}\)
Travel imposed on:
Side \(\mathrm{AB}\) \(\mathrm{DY}=0.\)
Side \(\mathrm{DA}\) \(\mathrm{DX}=0.\)
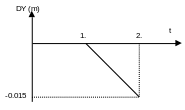
The movements vary over \(\mathrm{CD}\) gradually, over the interval \(t\mathrm{\in }\text{]}\mathrm{1,2}\mathrm{.}\text{]}\), following a ramp, as in the figure below: \(t=1.\) \(\mathrm{DY}=0.\)
\(t=2.\) \(\mathrm{DY}=-0.015\)
1.4. Initial conditions#
Initial conditions \((\mathrm{Pa})\)
\(\mathrm{SIXX}\) |
|
|
|
|
|
|
-2. E6 |
-2. E6 |
-2. E6 |
0.0 |
0.0 |
0.0 |
0.0 |
\(\mathrm{SIP}\) |
|
|
|
0.0 |
0.0 |
0.0 |
0.0 |