11. Modeling I#
11.1. Characteristics of modeling#
Plane stress modeling in plasticity using MFront (linear isotropic work hardening plasticity). The DeBorst algorithm is activated.
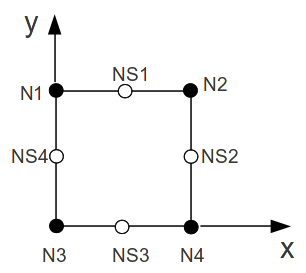
Dirichlet condition (keyword DDL_IMPO):
Node \(\mathrm{N04}\), \(x=y=0\),
Knots \(\mathrm{N02}\), \(\mathit{NS2}\) \(x=0\).
Neumann condition, surface forces (keyword FORCE_CONTOUR):
on the faces (skin elements): (1, 2), (2, 4), (4, 3) and (3, 1).
11.2. Characteristics of the mesh#
Number of knots: 8
Number of meshes and types: 1 QUAD8, 4 SEG3
11.3. Tested sizes and results#
Following sheet 7461, we test in non-regression that the internal variables are not modified by the calculation of the energy.
Identification |
Reference type |
Reference value |
V7 at time \(A\) |
“NON_REGRESSION” |
0.020547265463595 |
Identification |
Reference type |
Reference value |
Tolerance |
\({\sigma }_{\mathrm{xx}}\) at the moment \(A\) |
“ANALYTIQUE” |
1,512E+002 |
|
\({\sigma }_{\mathrm{xy}}\) at the moment \(A\) |
“ANALYTIQUE” |
9,310E+001 |
|
\({\varepsilon }_{\mathrm{xx}}\) at the moment \(A\) |
“ANALYTIQUE” |
1.48297E-002 |
|
\({\varepsilon }_{\mathrm{xy}}\) at the moment \(A\) |
“ANALYTIQUE” |
1.36014E-002 |
|
\({\varepsilon }_{\mathrm{xx}}^{p}\) at the moment \(B\) |
“ANALYTIQUE” |
1.4054E-002 |
|
\({\varepsilon }_{\mathrm{xy}}^{p}\) at the moment \(B\) |
“ANALYTIQUE” |
1, 2981E-002 |
|
\({\varepsilon }_{\mathit{xx}}\) at the moment \(B\) |
“ANALYTIQUE” |
3,5265E-002 |
|
\({\varepsilon }_{\mathit{xy}}\) at the moment \(B\) |
“ANALYTIQUE” |
2,0471E-002 |
|
\({\varepsilon }_{\mathrm{xx}}^{p}\) at the moment \(B\) |
“ANALYTIQUE” |
3,3946E-002 |
|
\({\varepsilon }_{\mathrm{xy}}^{p}\) at the moment \(B\) |
“ANALYTIQUE” |
2,0250E-002 |
|
\(p\) at the moment \(B\) |
“ANALYTIQUE” |
4,23293E-002 |
|
Triaxiality rate \(\mathit{TRIAX}\) at time \(A\) |
“ANALYTIQUE” |
2.2800E-001 |
|
Triaxiality rate \(\mathit{TRIAX}\) at time \(B\) |
“ANALYTIQUE” |
3.25349E-001 |
|