3. Modeling A#

3.1. Characteristics of modeling#

3D modeling

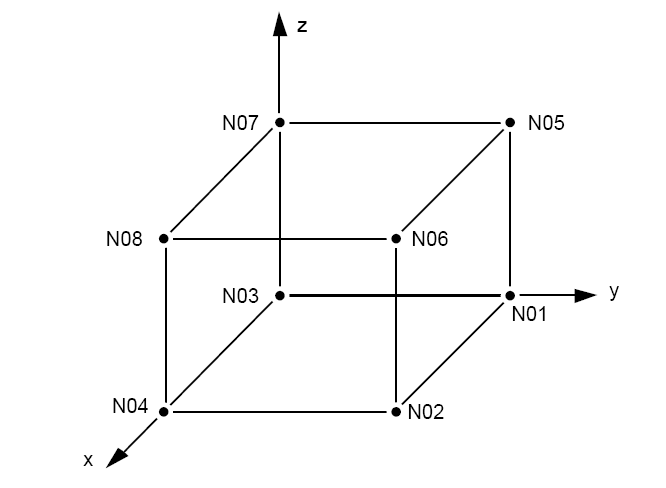
Loading and boundary conditions are modelled by:

Dirichlet condition (keyword DDL_IMPO):
Node \(\mathrm{N04}\), \(x=y=0\),
Node \(\mathrm{N08}\), \(x\mathrm{=}y\mathrm{=}z\mathrm{=}0\),
Node \(\mathrm{N02}\), \(x=0\),
Node \(\mathrm{N06}\), \(x=0\).
Neumann condition, surface forces (keyword FORCE_FACE):
on the faces (skin elements): \((\mathrm{1,}\mathrm{5,}\mathrm{6,}2)\), \((\mathrm{1,}\mathrm{5,}\mathrm{7,}3)\),, \((\mathrm{3,}\mathrm{4,}\mathrm{8,}7)\) and \((\mathrm{4,}\mathrm{8,}\mathrm{6,}2)\).

Number of knots: 8

Number of meshes and types: 1 HEXA8, 4 QUAD4

Identification	Reference type	Reference value	Tolerance
\({\sigma }_{\mathrm{xx}}\) at the moment \(A\)	“ANALYTIQUE”	1,512E+002	0.1%
\({\sigma }_{\mathrm{xy}}\) at the moment \(A\)	“ANALYTIQUE”	9,310E+001	0.1%
\(p\) at the moment \(A\)	“ANALYTIQUE”	2.0547E-002	0.1%
Triaxiality rate \(\mathit{TRIAX}\) at time \(A\)	“ANALYTIQUE”	2.2800E-001	0.1%
\({\varepsilon }_{\mathrm{xx}}\) at the moment \(A\)	“ANALYTIQUE”	1.48297E-002	0.1%
\({\varepsilon }_{\mathrm{xy}}\) at the moment \(A\)	“ANALYTIQUE”	1.36014E-002	0.1%
\({\varepsilon }_{\mathrm{xx}}^{p}\) at the moment \(A\)	“ANALYTIQUE”	1.40543E-002	0.1%
\({\varepsilon }_{\mathrm{xy}}^{p}\) at the moment \(A\)	“ANALYTIQUE”	1.29807E-002	0.1%
\(p\) at the moment \(B\)	“ANALYTIQUE”	4,23293E-002	1.0%
Triaxiality rate \(\mathit{TRIAX}\) at time \(B\)	“ANALYTIQUE”	3.25349E-001	0.1%
\({\varepsilon }_{\mathit{xx}}\) at the moment \(B\)	“ANALYTIQUE”	3,5265E-002	1,0%
\({\varepsilon }_{\mathit{xy}}\) at the moment \(B\)	“ANALYTIQUE”	2,0471E-002	1.0%
\({\varepsilon }_{\mathit{xx}}^{p}\) at the moment \(B\)	“ANALYTIQUE”	3,3946E-002	1.0%
\({\varepsilon }_{\mathit{xy}}^{p}\) at the moment \(B\)	“ANALYTIQUE”	2,0250E-002	1.0%

as well as the charge-discharge indicators:

Identification	Reference Type	Value	Tolerance
INDIC_ENER at the moment \(A\)	“ANALYTIQUE”	0	0.1%
INDIC_ENER at the moment \(B\)	“ANALYTIQUE”	3,26E-002	3,0%
INDIC_SEUIL at the moment \(A\)	“ANALYTIQUE”	0	0.1%
INDIC_SEUIL at the moment \(B\)	“ANALYTIQUE”	3,26E-002	3,0%
INDIC_ENER at the moment \(C\) (full discharge)	“ANALYTIQUE”	4,69E-002	3,0%
INDIC_SEUIL at time \(C\) (full discharge)	“ANALYTIQUE”	1.0	1.0%
DERA_ELNO/RADI_Và the moment 0.1	“ANALYTIQUE”	0.0	1.0%

We only calculate the energies, and we compare with case VMIS_ISOT_LINE:

Identification	Reference Type	Value	Tolerance
ETOT_ELGA/TOTALE at the moment 0.1	“AUTRE_ASTER”	1.16403E-03	0.1%
ETOT_ELGA/TOTALE at the moment 0.9	“AUTRE_ASTER”	1.84340	0.1%
ETOT_ELGA/TOTALE at the moment 2.0	“AUTRE_ASTER”	9.58487	0.1%
ETOT_ELGA/TOTALE at the moment 3.0	“AUTRE_ASTER”	9.40794	0.1%
ETOT_ELNO/TOTALE at the moment 0.1	“AUTRE_ASTER”	1.16403E-03	0.1%
ETOT_ELNO/TOTALE at the moment 0.9	“AUTRE_ASTER”	1.84340	0.1%
ETOT_ELNO/TOTALE at the moment 2.0	“AUTRE_ASTER”	9.58487	0.1%
ETOT_ELNO/TOTALE at the moment 3.0	“AUTRE_ASTER”	9.40794	0.1%
ETOT_ELEM/TOTALE at the moment 0.1	“AUTRE_ASTER”	1.16403E-03	0.1%
ETOT_ELEM/TOTALE at the moment 0.9	“AUTRE_ASTER”	1.84340	0.1%
ETOT_ELEM/TOTALE at the moment 2.0	“AUTRE_ASTER”	9.58487	0.1%
ETOT_ELEM/TOTALE at the moment 3.0	“AUTRE_ASTER”	9.40794	0.1%
ETOT_NOEU/TOTALE at the moment 3.0	“AUTRE_ASTER”	9.40650	0.1%

The discharge DCHA_V and radiality loss DCHA_R indicators are tested in mesh \(\mathit{CUBE}\):

We test in mesh \(\mathit{CUBE}\) at Gauss point 1:

The discharge indicator IND_DCHA, which allows you to know if the discharge remains elastic or if there would be a risk of plastification if pure kinematic work hardening was used,
Indicator VAL_DCHA which indicates the proportion of criteria output.