5. C modeling#
5.1. Characteristics of modeling#
Shell modeling DKT - DKQ
5.2. Geometry#
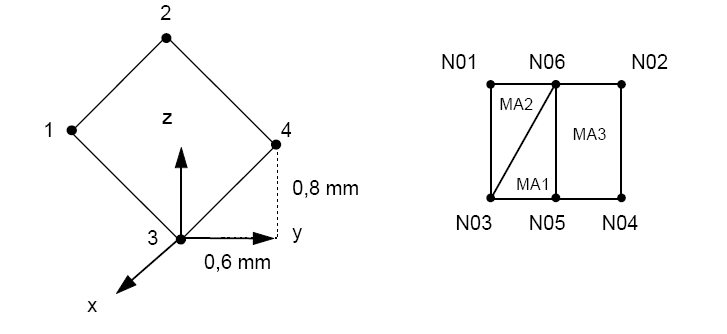
The dimensions of the structure do not change in relation to the reference problem; only its orientation differs.
Node coordinates:
Knots |
\(x\) |
|
|
\(\mathrm{N01}\) |
0 |
—0.8 |
0.6 |
\(\mathrm{N02}\) |
0 |
—0.2 |
1.4 |
\(\mathrm{N03}\) |
0 |
0 |
0 |
\(\mathrm{N04}\) |
0 |
0.6 |
0.8 |
\(\mathrm{N05}\) |
0 |
0.3 |
0.4 |
\(\mathrm{N06}\) |
0 |
—0.5 |
1 |
Boundary conditions:
_F (TOUT =” OUI “, DX=0.0,),), LIAISON_DDL =_F (NOEUD =( “NO2”, “NO2”,), DDL =( “DY”, “DZ”,), COEF_MULT =( 0.75,1.0,), COEF_IMPO =0.0,),);
Charging:
Surface forces (keyword FORCE_ARETE) are imposed on the faces (SEG2 skin elements) \((\mathrm{1,2})\), \((\mathrm{2,4})\), \((\mathrm{4,3})\) and \((\mathrm{3,1})\).
Specificity DKT and DKQ:
Two layers in the thickness for plasticity.
5.3. Characteristics of the mesh#
Number of knots: 6
Number of meshes and types: 2 TRIA3 and 1 QUAD4
5.4. Tested sizes and results#
The movements tested are those of the reference problem taking into account the rotation of the structure.
Deformations, stresses, and generalized forces are tested in the user coordinate system defined by the ANGL_REP command. The values are therefore those given by the reference problem.
The values are tested at point \(A\) of the \(\mathrm{OA}\) loading path. We test as follows:
Travel (DEPL). They are easily deduced from the reference solution since the deformation is homogeneous.
Identification |
Reference |
% Tolerance |
\(\mathrm{DY}\) \(\mathrm{N01}\) |
1.86722 10—2 |
1.00E-004 |
\(\mathrm{DZ}\) \(\mathrm{N01}\) |
—3.25413 10—2 |
1.00E-004 |
\(\mathrm{DY}\) \(\mathrm{N06}\) |
1.224 10—2 |
1.00E-004 |
\(\mathrm{DZ}\) \(\mathrm{N06}\) |
—1.88485 10—2 |
1.00E-004 |
\(\mathrm{DY}\) \(\mathrm{N02}\) |
5.80782 10—3 |
1.00E-004 |
\(\mathrm{DZ}\) \(\mathrm{N02}\) |
—4.35586 10—3 |
1.00E-004 |
Constraints (SIGM_ELNO).
Identification |
Reference |
% Tolerance |
\(\mathrm{SIXX}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
1.512 102 |
1.0 |
\(\mathrm{SIXY}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
93.1 |
1.0 |
\(\mathrm{SIXX}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
1.512 102 |
1.0 |
\(\mathrm{SIXY}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
93.1 |
1.0 |
\(\mathrm{SIXX}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
1.512 102 |
1.0 |
\(\mathrm{SIXY}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
93.1 |
1.0 |
\(\mathrm{SIXX}\) \(\mathrm{MA3}\) \(\mathrm{N02}\) |
1.512 102 |
1.0 |
\(\mathrm{SIXY}\) \(\mathrm{MA3}\) \(\mathrm{N02}\) |
93.1 |
1.0 |
Generalized efforts by elements at the nodes (EFGE_ELNO).
Identification |
Reference |
% tolerance |
\(\mathrm{NXX}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
3.024 102 |
1.0 |
\(\mathrm{NXY}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
1.862 102 |
1.0 |
\(\mathrm{NXX}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
3.024 102 |
1.0 |
\(\mathrm{NXY}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
1.862 102 |
1.0 |
\(\mathrm{NXX}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
3.024 102 |
1.0 |
\(\mathrm{NXY}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
1.862 102 |
1.0 |
\(\mathrm{NXX}\) \(\mathrm{MA3}\) \(\mathrm{N02}\) |
3.024 102 |
1.0 |
\(\mathrm{NXY}\) \(\mathrm{MA3}\) \(\mathrm{N02}\) |
1.862 102 |
1.0 |
Elemental deformations at the nodes from displacements (EPSI_ELNO).
Identification |
Reference |
% tolerance |
\(\mathrm{EPXX}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
1.48297 10—2 |
0.01 |
\(\mathrm{EPYY}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
—7.25977 10—3 |
0.01 |
\(\mathrm{EPXY}\) \(\mathrm{MA2}\) \(\mathrm{N01}\) |
1.36014 10—2 |
0.01 |
\(\mathrm{EPXX}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
1.48297 10—2 |
0.01 |
\(\mathrm{EPYY}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
—7.25977 10—3 |
0.01 |
\(\mathrm{EPXY}\) \(\mathrm{MA1}\) \(\mathrm{N03}\) |
1.36014 10—2 |
0.01 |
\(\mathrm{EPXX}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
1.48297 10—2 |
0.01 |
\(\mathrm{EPYY}\) \(\mathrm{MA2}\) \(\mathrm{N03}\) |
—7.25977 10—3 |
0.01 |
\(\mathrm{EPXY}\) \(\mathit{MA}2\) \(N03\) |
1.36014 10—2 |
0.01 |
\(\mathit{EPXX}\) \(\mathit{MA}3\) \(N02\) |
1.48297 10—2 |
0.01 |
\(\mathit{EPYY}\) \(\mathit{MA}3\) \(N02\) |
—7.25977 10—3 |
0.01 |
\(\mathit{EPXY}\) \(\mathit{MA}3\) \(N02\) |
1.36014 10—2 |
0.01 |
\(\mathit{EPXX}\) \(\mathit{MA}3\) \(N04\) |
1.48297 10—2 |
0.01 |
\(\mathit{EPYY}\) \(\mathit{MA}3\) \(N04\) |
—7.25977 10—3 |
0.01 |
\(\mathit{EPXY}\) \(\mathit{MA}3\) \(N04\) |
1.36014 10—2 |
0.01 |