1. Reference problem

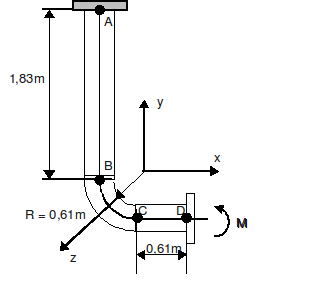
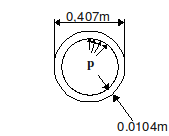
1.1. Geometry

1.2. Material properties

The properties of the material from which the pipe is made are:

\(E\mathrm{=}193.{10}^{9}\mathit{Pa}\)	Young’s module
\(\nu \mathrm{=}0.2642\)	Poisson’s ratio

	Constraint \(\mathrm{Pa}\)	Plastic Deformation \({\varepsilon }_{p}\)
	2.72E+08 3.46E+08 3.79E+08 4.04E+08 4.24E+08 5.28E+08	0.00000 0.00473 0.01264 0.01264 0.02836 0.04910 0.10500

1.3. Boundary conditions and loads

• Boundary conditions:

◦ Recessed section \(A\)

◦ Rigid section \(D\) (no deformation of the section)

• Loading: we are looking for the successive states of equilibrium under the following loads:

◦ Step A: \(0\mathrm{=}t<{t}_{1}\)

▪ the pressure varies from \(0\) to \(3.45{10}^{6}\mathrm{Pa}\)

▪ The strength (shape effect) at point \(D\) varies from \(0\) to \(4.0414{10}^{5}N\)

▪ The moment sucks

◦ Step B: \({t}_{1}\mathrm{=}t<{t}_{2}\)

▪ the pressure is constant and is \(3.45{10}^{6}\mathrm{Pa}\)

▪ the force (shape effect) at point \(D\) is constant and is equal to \(4.0414{10}^{5}N\)

▪ the timing varies from \(0\) to \(2.534{10}^{5}\mathit{N.m}\)