3. Modeling A#

3.1. Characteristics of modeling#

Modeling POU_D_TGM (140 elements)/DIS_TR (22 elements)

The modeling of bolted assemblies is ensured by discretes whose stiffness is fixed in a fixed manner. The eccentricities of the attachment points are taken into account (which explains why the elements are not concurrent). The model is obtained from the pre-processor EVEREST.

The load case is the first (\(\mathit{C1}\)).

3.2. Characteristics of the mesh#

Number of knots: 191

Number of meshes and types: 162 SEG2 (including 22 of zero length for discrete ones)

3.3. Characteristics of the cross section (fibers)#

Number of fibers: 40 (divided into 2 in the thickness and into 10 in the length of the wings)

3.4. Tested sizes and results#

3.4.1. Tested values#

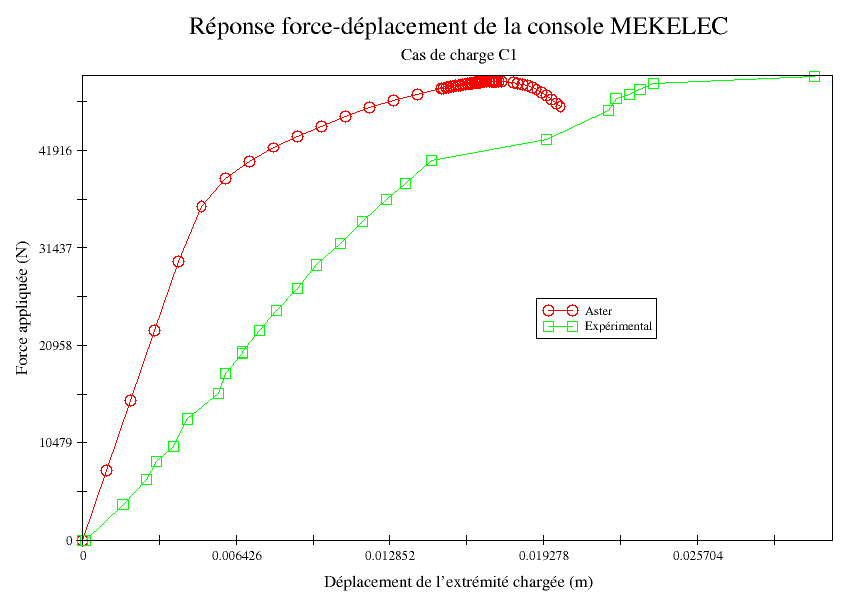
The value tested is the estimated ruin load for the structure. Since the reference results are experimental, comparisons are combined with non-regression tests. The ruin load for the design is defined as being the maximum value taken by the force applied to the structure.

Reminder: we pilot the structure while moving, so we observe softening.

Load case	Reference	Reference type	Tolerance
C1	49.9	“SOURCE_EXTERNE”	10%

3.4.2. Graphical results of modeling A#

3.4.3. notes#

The numerical response of the structure is obtained by controlling the loaded node while moving, this makes it possible to observe the softening due to the ruin and therefore to be able to test the maximum value of the control state (parameter ETA_PILOTAGE).

The ruin load for this load case is correctly estimated, however it is noted that the experimental response and the numerical response differ widely, in particular because of an elastic slope that is greatly overestimated in the Aster calculation. The rigidity of the structure is in fact not well transcribed in the model: the gussets that make it possible to ensure the assemblies at the head and foot of the console are supposed to behave rigidly when they are plates.

However, it can be observed that the overall pattern of the experimental and numerical responses is the same with a good description of the change in slope (plastification at the top of the console) and then of the limit load (horizontal tangent to the force-displacement curve).