1. General characteristics

1.1. Geometry

The geometry is identical to that of test cases SSNL119 and SDLL130 except for the longitudinal reinforcements, which are all identical here: these are four \(\mathit{HA32}\).

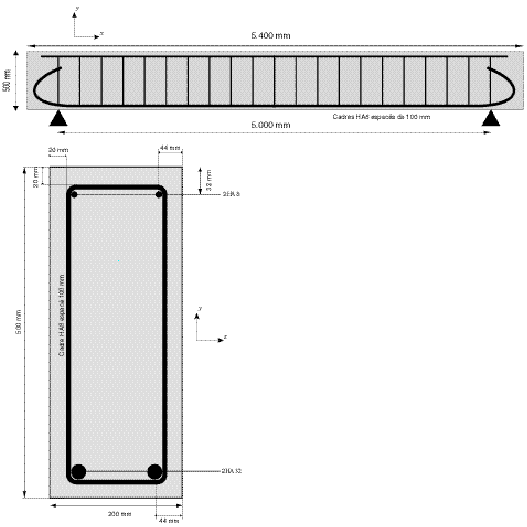
Figure 1.1-a: g**structure geometry**

NB: transverse reinforcements are not taken into account in the calculations.

1.2. Material properties

For modeling A:

For concrete, Mazars’s law of behavior in its 1D version:

Elasticity part:

\(E\mathrm{=}3.72720E+10\), \(\mathit{NU}\mathrm{=}2.0E-01\), \(\mathit{RHO}\mathrm{=}2.40E+03\),

Non-linear part:

\(\mathit{AC}\mathrm{=}1.71202987\), \(\mathit{BC}\mathrm{=}2.01163780E+03\), \(\mathit{BT}\mathrm{=}1.21892353E+04\),

\(\mathit{BETA}\mathrm{=}1.10\), \(\mathit{AT}\mathrm{=}1.00\), \(\mathit{EPSD0}\mathrm{=}8.20396008E-05\),

For modeling B:

Concrete:

Young’s module: \(E\mathrm{=}37272\mathit{MPa}\)

Poisson’s ratio: \(\nu =0.2\)

Tensile elasticity threshold: \({\sigma }_{\mathrm{ft}}=3.9\mathrm{MPa}\)

Threshold of elasticity in compression: \({\sigma }_{\mathrm{fc}}=38.3\mathrm{MPa}\)

For A and B models:

ecro_line law of behavior for steel:

\(E=200000\mathrm{MPa}\), \(\nu =0.33\), \({\sigma }_{e}=400\mathrm{MPa}\), \({E}_{T}=3280\mathrm{MPa}\), \(\rho =7800\mathrm{kg}/{m}^{3}\)

Damping: Rayleigh type (\(\alpha K+\beta M\)), with \(\text{5\%}\) on modes 1 and 2.

1.3. Boundary conditions and loads

Simple press in \(B\): \(\mathrm{dy}=0\)

Press « double » in \(A\): \(\mathrm{dx}=\mathrm{dy}=0\)

To avoid out-of-plane modes, the following degrees of freedom are blocked all over the beam: \(\mathrm{rx}=\mathrm{ry}=\mathrm{dz}=0\)

Loading: earthquake ac_s2_c_1 [Figure], in axis \(\mathit{OY}\) applied to both supports, with a signal amplification factor of 45.

Figure 1.3-a: a ac_s2_c_1 accelerogram imposed on the structure