6. D modeling#
6.1. Characteristics of modeling#
Modeling DKT. We mesh only half of the cylinder (symmetry with respect to plane \(y=0\)) 30 mesh QUAD4 in the height and 60 on the half-circumference.
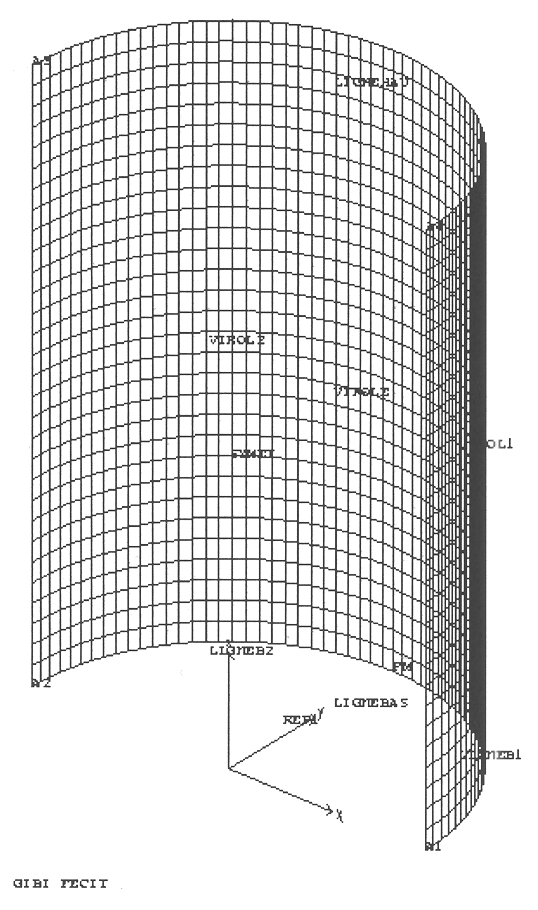
6.2. Characteristics of the mesh#
Number of knots: 1894
Number of meshes and types: 1800 QUAD4
Note:
To obtain a precise solution to this problem, it is necessary to use a fairly refined mesh (here 1800 QUAD4).
The following errors are observed as a function of discretization:
Number of items |
Maximum displacement error |
450 QUAD4 |
|
1800 QUAD4 |
|
900 TRIA3 |
|
3600 TRIA3 |
|
It can be seen that for this problem, meshing in quadrangles is preferable.
6.3. Tested values#
Isotropic material
Value |
Identification |
Reference |
\(\mathrm{Ur}(z=0)\) |
|
5.8018E—05 |
\(\mathrm{Ur}(z=0)\) |
|
5.8018E—05 |
\(\mathrm{Ur}(z=0)\) |
|
—5.8018E—05 |
\(\mathrm{Uz}(z=L)\) |
|
—2.4429E—05 |
\(\mathrm{Uz}(z=L)\) |
|
—2.4429E—05 |
\(\mathrm{SigmaTT}(z=0)\) |
|
2.1375E+06 |
Orthotropic material
Value |
Identification |
Reference |
\(\mathrm{Ur}(z=0)\) |
|
5.8018E—05 |
\(\mathrm{Ur}(z=0)\) |
|
5.8018E—05 |
\(\mathrm{Ur}(z=0)\) |
|
—5.8018E—05 |
\(\mathrm{Uz}(z=L)\) |
|
—6.10714E—06 |
\(\mathrm{Uz}(z=L)\) |
|
—6.10714E—06 |
\(\mathrm{SigmaTT}(z=0)\) |
|
2.1375E+06 |