14. N modeling#
14.1. Characteristics of modeling#
COQUE_SOLIDE elements with hexahedra (quarter plate modeling)
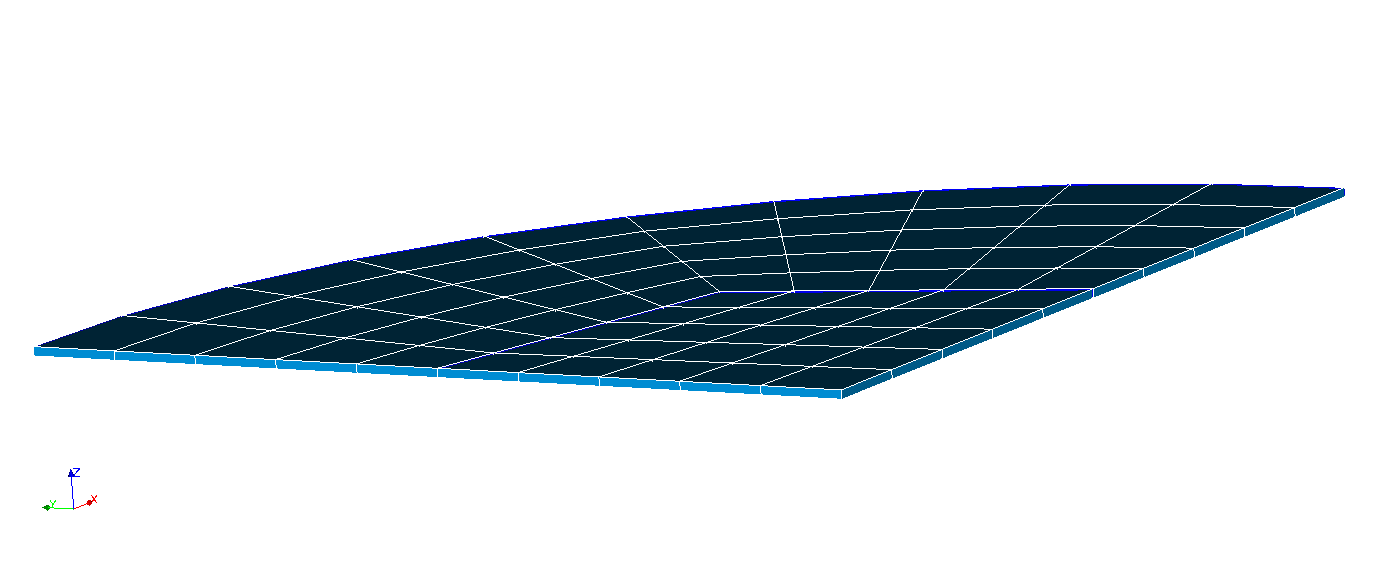
Boundary conditions:
On the face corresponding to the plane X=0, symmetry condition \(\mathit{DX}=0\)
On the face corresponding to the plane Y=0, symmetry condition \(\mathit{DY}=0\)
On the face corresponding to the outer quarter circle: embedding condition \(\mathit{DX}=\mathit{DY}=\mathit{DZ}=0\)
Loading
On the upper side: distributed pressure \(p=0.01172\mathit{MPa}\)
14.2. Characteristics of the mesh#
Number of knots: 182
Number of meshes and types: 75 HEXA9
14.3. Tested sizes and results#
Coordinates of Gauss points (COOR_ELGA): test of the mesh at the center of the disk (GROUP_MA =”CellMiddle”). Lobatto diagram with five integration points in the thickness, in the middle of the mesh.
For \(\mathit{Pg}=1\), the face below, coordinates of the Gauss point:
Identification |
Reference type |
Reference values (mm) |
Tolerance \((\text{\%})\) |
\(X\) |
“ANALYTIQUE” |
4, 9 |
0 |
\(Y\) |
“ANALYTIQUE” |
4.9 |
0 |
\(Z\) |
“ANALYTIQUE” |
0 |
0 |
For \(\mathit{Pg}=3\), at half the thickness, coordinates of the Gauss point:
Identification |
Reference type |
Reference values (mm) |
Tolerance \((\text{\%})\) |
\(X\) |
“ANALYTIQUE” |
4, 9 |
0 |
\(Y\) |
“ANALYTIQUE” |
4.9 |
0 |
\(Z\) |
“ANALYTIQUE” |
0.5 |
0 |
For \(\mathit{Pg}=5\), the top face, coordinates of the Gauss point:
Identification |
Reference type |
Reference values (mm) |
Tolerance \((\text{\%})\) |
\(X\) |
“ANALYTIQUE” |
4, 9 |
0, |
\(Y\) |
“ANALYTIQUE” |
4.9 |
0 |
\(Z\) |
“ANALYTIQUE” |
1.0 |
0 |
Vertical movement in the center of the plate:
Identification |
Reference type |
Reference values |
Tolerance \((\text{\%})\) |
DZ |
“ANALYTIQUE” |
\(-\mathrm{2.09114}\mathit{mm}\) |
|
Constraint \({\sigma }_{\mathit{zz}}\) at the middle node of the quarter circle (SIEF_NOEU):