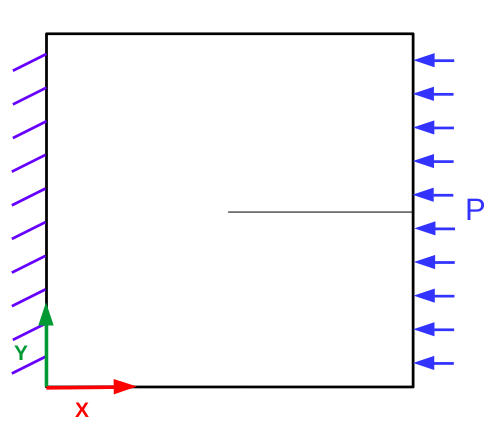
1. Reference problem#
1.1. Geometry#
Consider a square with side \(1m\) crossed by a horizontal crack:
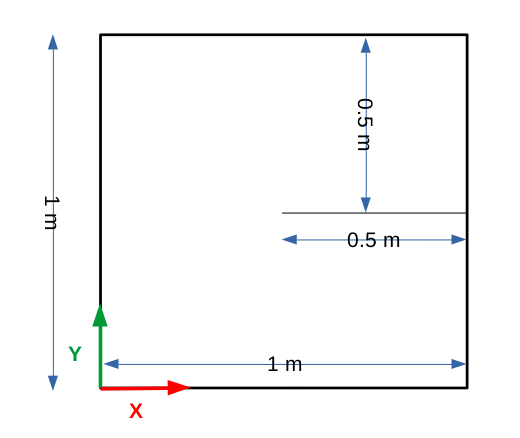
The crack is defined by the normal « level set » \({l}_{n}(Y)=Y-0.5\) and the tangent \({l}_{t}(X)=-X+0.5\).
1.2. Material properties#
The material is isotropic elastic whose properties are:
\(E=100000\mathrm{MPa}\)
\(\nu =0.0\)
1.3. Boundary conditions and loads#
1.3.1. Dirichlet boundary conditions#
For the A modeling, Dirichlet boundary conditions are imposed along the entire contour of the square corresponding to the asymptotic opening mode in I [1] mode. We then have:
\({u}_{X}=\frac{1}{2\mu }\sqrt{\frac{r}{2\pi }}{K}_{I}\mathrm{cos}\frac{\theta }{2}(\kappa -\mathrm{cos}\theta )\) and \({u}_{Y}=\frac{1}{2\mu }\sqrt{\frac{r}{2\pi }}{K}_{I}\mathrm{sin}\frac{\theta }{2}(\kappa -\mathrm{cos}\theta )\),
with:
\(\mu =\frac{E}{2(1+\nu )}\) and \(\kappa =3-4\nu\) in plane constraints,
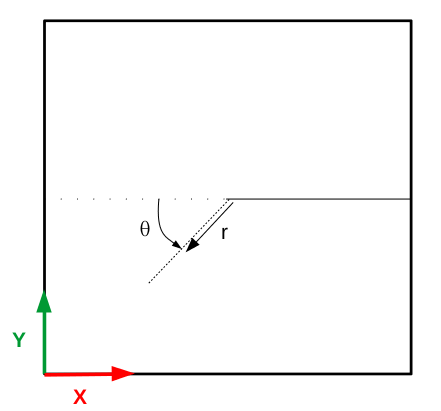
\(r\) and \(\theta\) are the polar coordinates as defined in the following figure:
With \(\nu =0.0\) and \({K}_{I}=1\), we finally impose:
\({u}_{X}=\frac{1}{E}\sqrt{\frac{r}{2\pi }}\mathrm{cos}\frac{\theta }{2}(3-\mathrm{cos}\theta )\) and \({u}_{Y}=\frac{1}{E}\sqrt{\frac{r}{2\pi }}{K}_{I}\mathrm{sin}\frac{\theta }{2}(3-\mathrm{cos}\theta )\).
1.3.2. Neumann boundary conditions#
For modelling B, Neumann boundary conditions are imposed. A uniform compression \(P=-20\mathit{MPa}\) is imposed on the right edge while the left edge is embedded.